第一章 平流输送

1. 理解平流输送

平流输送（Advection）是指在流体中，物质随着流体的流动而传输的过程。平流输送是空气质量数值模式(CTM)中最基本的过程之一。而平流方程只是连续性方程的特殊情况。

连续性方程（continuity equation）是描述守恒量传输行为的偏微分方程。在流体力学里，连续性方程表明，在任何稳定态过程中，质量进入物理系统的速率等于离开的速率。质量连续性方程的微分形式为 $$\frac{\partial c}{\partial t} = - \nabla \cdot (\mathbf{v} c) \tag {1.1} \label {1.1}$$

其中$c$ 表示污染物的浓度（质量浓度，如$\mu g/m^3$），$\mathbf{v}$ 为速度向量场，$\mathbf{v} c$ 为通量。

数值模式中的平流过程，就是在已知速度向量场的情况下，求解大气连续性方程。

通常给定的风场是离散的，同时，我们也需要通过数值方式来求解该方程。

我们通过一个简单推导来理解如何对平流过程进行数值求解。

首先把散度符号展开

$$\frac{\partial c}{\partial t} = - (\frac{\partial (u c)}{\partial x} + \frac{\partial (v c)}{\partial y} + \frac{\partial (w c)}{\partial z}) \tag {1.2}$$

我们考虑一维的平流输送方程 $$\frac{\partial c}{\partial t} = - \frac{\partial (u c)}{\partial x} \tag {1.3} \label{1.3}$$

一维的平流输送方程有两个需要离散化处理的变量，分别为 ${\partial x}$ 和 ${\partial t}$ 。

我们首先对公式\ref{1.3} 进行空间上的离散处理。在离散化过程中，我们假定空间离散式均匀的（既等网格）。

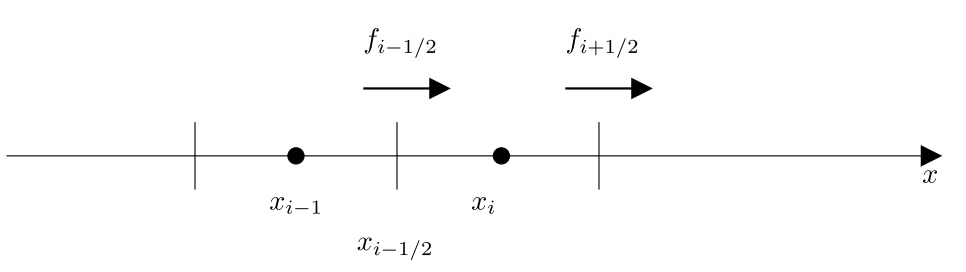
那么公式可以改写为 $$\frac{\partial c_{i}}{\partial t} = \frac{f_{i-1/2}-f_{i+1/2}}{\Delta x} \tag {1.4} \label {1.4}$$

其中$f_{i-1/2}$ 为格子$i-1$ 和格子$i$ 之间的边界($i-1/2$) 处的通量（单位时间，单位面积通过的物质量的：$\mu g/m^2s$），其物理含义为该格子浓度的变化等于流入流出的量。其中通量的公式为

$$f_{i-1/2} = u_{x_{i-1/2}} \times c_{x_{i-1/2}} \tag {1.5} \label {1.5}$$

将公式\ref{1.5}带入到公式\ref{1.4}中 $$\frac{\partial c_{i}}{\partial t} = \frac {u_{x_{i-1/2}} \times c_{x_{i-1/2}} - u_{x_{i+1/2}} \times c_{x_{i+1/2}}} {\Delta x} \tag {1.6} \label{1.6}$$

再对公式\ref{1.6} 时间进行离散化，如果采用简单的显示欧拉方法，即可得到

$$\frac{c_{x_{i}}^{n+1}-c_{x_{i}}^{n}}{\Delta t} = \frac {u_{x_{i-1/2}}^n \times c_{x_{i-1/2}}^n - u_{x_{i+1/2}}^n \times c_{x_{i+1/2}}^n} {\Delta x} \tag {1.7}$$

其中$n$ 为时间索引，整理一下（Godunov's scheme）：

$$c_{x_{i}}^{n+1} = c_{x_{i}}^{n} + (\frac {u_{x_{i-1/2}}^n \times c_{x_{i-1/2}}^n - u_{x_{i+1/2}}^n \times c_{x_{i+1/2}}^n} {\Delta x}) \times {\Delta t} \tag {1.8} \label {1.8}$$

由以上公式可知，计算平流过程最关键的步骤就是如何获得边界处的通量（边界处的浓度是关键）。

2. 需要考虑的问题

似乎根据公式\ref{1.8} 就能较好的求解出平流对浓度的影响。 如果仔细想想，我们会面对四个额外的问题。

首先，我们观察等号右边的中间项（把括号展开, 并稍加整理） $$(\frac {u_{x_{i-1/2}}^n \times {\Delta t}} {\Delta x}) \times c_{x_{i-1/2}}^n \tag {1.9} \label {1.9}$$

我们需要意识到，公式\ref{1.9} 中存在一个假设，该公式计算的浓度增量是从格子$i-1$ 输送到格子$i$ ，注意这个增量会最终叠加在格子$i$ 中，公式\ref{1.8} 中只涉及对$c_{x_{i}}$ 的更新，那么有没有一种可能。风速太大了，吹出了格子$i$ 呢！

当然有可能，所以我们要对数值求解方案施加限制

$$\frac {u_{x_{i-1/2}}^n \times {\Delta t}} {\Delta x} < 1 \tag {1.10}$$

这就是 Courant-Friedrichs-Lewy（CFL） 条件。

我们在设置${\Delta x}$ 和${\Delta t}$ 的时候，应该尽量保证这个条件，这样积分才具有稳定性。

另外一个我们需要关注的问题是数值扩散，由于充分混合的假设，很容易使得平流方案计算的扩散速度大于物理上的实际扩散速度。

想像一下，如果一个格子很大，比如 $81km*81km$ ，从西边界吹入一个高浓度的值，这个高浓度值会瞬间在整个格子里面混合，也就是说这个增量一下就会吹到东边界，肯定比实际扩散的要快一些（因此如何获得边界上的值，是一个比较有挑战的事情，好的方案可以减缓数值扩散）。

然后我们需要关注的事情是质量的一致性（污染物浓度的行为和空气密度的行为不一致，模拟空气通量的风场和模拟污染物通量的风场不一致），空气质量模式往往采用离线模拟的方式（气象场先模拟，再模拟CTM），并且CTM的网格和原始的气象网格存在差异，不同的离散方案(时间和空间)和插值都会导致质量一致性的出现问题。

如果用质量混合比来表示平流方程，设$C = \frac {c}{\rho}$。

那么（链式法则 => 带入公式\ref{1.1} => 带入C的定义 => 链式法则）

$$\begin{align*} \frac{\partial C}{\partial t} &= \frac{1}{\rho}\frac{\partial c}{\partial t} - \frac{c}{\rho^2}\frac{\partial \rho}{\partial t} \\ &= -\frac{\nabla \cdot (\mathbf{v}c)}{\rho} + \frac{c}{\rho^2} {\nabla \cdot (\mathbf{v} \rho)} \\ &= {-\frac{\nabla \cdot (\rho \mathbf{v}C) + C{\nabla \cdot (\mathbf{v} \rho)}} {\rho}} \\ &= -( \mathbf{v} \cdot \nabla C + \frac{C}{\rho} {\nabla \cdot (\mathbf{v} \rho)}) + \frac{C}{\rho} {\nabla \cdot (\mathbf{v} \rho)}\\ &= - \mathbf{v} \cdot \nabla C \tag {1.11} \end{align*}$$

注意，最终的结论是 $$\frac{\partial C}{\partial t} = - \mathbf{v} \cdot \nabla C \tag {1.12} \label {1.12}$$

要满足质量守恒，公式\ref{1.12}只有唯一的一个解，就是$C(t) = k$，其中$k$ 为常数，也就是说，污染物浓度的变化要和密度变化协调一致（其实很好理解，浓度和空气密度都是同样的方程支配平流输送，变化的步调应该是协调一致的）。

最后我们需要关注的事情是质量守恒性，不能因为平流过程的计算，增加或者减少了物质，平流只是把物质从一个地方输送到另一个地方。质量不守恒一般是怎么引发的呢？

其中一个非常重要的因数就是网格的size不一样大（体积、面积、长度）。在实际的数值模式中，网格不一致的原因有很多种，包括 1）非均一网格；2）气压垂直层；3）地图投影的形变。

那么为什么网格不一致，会导致质量不守恒呢，仔细观察公式\ref{1.8} 就可以方向，物质从左边的格子输送到右边，是以浓度增量的方式更新网格浓度，浓度是强度量，如果左边的格子远小于右边，比如左边为$1 m^3$，右边为$10 m^3$，如果左边网格损失$1 \mu g/m^3$，物质的量损失了$1 \mu g$。按照公式，右边的网格增加$1 \mu g/m^3$，但是物种的量却增加了$10 \mu g$。

3. 分段多项式平流方案

分段多项式平流方案（Piecewise Parabolic Method，PPM）是一种用于求解流体动力学方程的数值方法，特别是在处理高分辨率、具有激波等间断的流体问题时表现出色。

PPM具有三阶精度，广泛用于主流的空气质量模式中（CMAQ、CAMx 等）。该方案适用于非结构化网格（结构化网格只是非结构化网格的特例），为了思路更加、简单清楚，在本文档的推导过程中，只采用等网格间距的设定，且只考虑一维的情况。

在浓度的离散表示中，网格浓度为该网格的平均浓度。根据定义，我们得到以下公式 $$c_i^n = \frac{1}{\Delta x} \int_{x_{i-1/2}}^{x_{i+1/2}} c(x, t^n) dx \tag {2.1} \label {2.1}$$

其中，$c_i^n$表示第$i$个格子在$t^n$时刻的浓度。$c(x, t^n)$为$t^n$时刻浓度在空间的分布函数，当然$c(x, t^n)$ 函数是未知的，也是无法精确给出的。

可以针对某个时刻 $$c_i^n = \frac{1}{\Delta x} \int_{x_{i-1/2}}^{x_{i+1/2}} c^n(x) dx \tag {2.2} \label {2.2}$$

公式\ref{2.2} 暗含了一种检查方案，我们假定已知$c^0(x)=p(x)$ (函数形式可以随意给定，比如$p(x)=sin(x)$)，且速度确定并已知，那么可以算出每个网格在任意时间的精确值(函数的形态不变，只是沿着x轴随时间平移)

$$c_i^n = \frac{1}{\Delta x} \int_{x_{i-1/2}}^{x_{i+1/2}} p(x-ut^n) dx \tag {2.3} \label {2.3}$$

要进行通量计算，需要知道每个时刻的$c^n$，不同方案对$c^n$ 的函数形式给出了不同的假设。

比如零阶精度假定格子内的浓度均匀分布（分布函数为常数，格子边界处浓度等于平均浓度），一阶精度假定函数形式为线性的（两个格子的线性插值），而PPM假定该函数为多项式。

PPM方案采用分段连续的二次多项式方案来表示每个格子在不同时间的$c^n$。为了方便，在后续过程中，省略时间的角标，也就是只考虑某个时次的情况，在每个网格中的二次多项式为（假定左右边界的浓度值已知，该值在后续的推导过程中确认）

$$\begin{align*} c(x) &= c_{x_{i-1/2}} + \xi(\Delta x + (1-\xi)c_{6,i}) \quad 0 \le \xi \le 1 \\ c(x) &= c_{x_{i-1/2}} + \frac{x-x_{i-1/2}}{\Delta x}(\Delta c_i + \frac{x_{i+1/2}-x}{\Delta x}{c_{6,i}}), \quad x_{i-1/2} \le x \le x_{i+1/2} \tag {2.4} \label {2.4} \end{align*}$$ 其中 $$\begin{align*} \xi &= \frac{x-x_{i-1/2}}{\Delta x} \\ \Delta c_i &= c_{x_{i+1/2}} - c_{x_{i-1/2}} \\ \end{align*}$$

从公式\ref{2.4} 中很容易看出，构造的多项式在左右边界是连续（带入$x=x_{i-1/2}$，或者带入$x=x_{i+1/2}$），公式\ref{2.4}中只有一个未知参数$c_{6,i}$。

如何计算$c_{6,i}$，我们需要考虑其他已知条件，我们知道该网格的平均浓度$c_{i}$。

对公式\ref{2.4} 两边进行积分求，并带入公式\ref{2.2} ，可到$c_{6,i}$的表达式

$$c_{6,i} = 6(c_i- \frac{1}{2}(c_{x_{i+1/2}} + c_{x_{i-1/2}}) ) \tag {2.5} \label {2.5}$$

可以采用sympy 进行公式推导，并且进行验证。

from sympy import *
init_printing()

ci = symbols('c_i', real=true, constant=true)  # 网格平均浓度
cL = symbols('cL_i', real=true, constant=true) # 左边界浓度
cR = symbols('cR_i', real=true, constant=true) # 右边界浓度

x = symbols('x')
xL = symbols('xL_i', real=true, constant=true) # 左边界位置
xR = symbols('xR_i', real=true, constant=true) # 右边界位置

c6 = symbols('c6_i', real=true, constant=true) # 参数c6

f = cL + (x-xL)/(xR-xL) * (cR-cL + c6*((xR-x)/(xR-xL))) # 公式2.4
fR = integrate(f, (x, xL, xR))/(xR-xL) # 公式2.2的左边, factor(fR)

solveset(Eq(fR, ci), c6) # 公式2.2

我们在推导公式\ref{2.4}，假定了网格之间边界处的浓度已知，但目前并不知道该值。那么，该如何获得$c_{x_{i+1/2}}$ 呢？

在PPM中，通过四次多项式（quartic polynomial）描述浓度在空间的积分函数，从而来求解$c_{x_{i+1/2}}$ 的分布。

我们首先定义浓度在空间的积分函数： $$C(x_{i+1/2}) = \int^{x_{i+1/2}} c(x)dx = C_{i+1/2}= \sum_{k \le i} c_i \Delta x \tag {2.6} \label {2.6}$$

而网格边界处的浓度$c_{x_{i+1/2}}=\frac{dC}{dx}|x=x_{i+1/2}$

从公式\ref{2.6} 可知$C(x)$ 在边界处的值是已知，现在要求边界处的浓度值，我们需要知道C(x)的函数形式，在PPM中，用5个点（$C_{i+1/2}, x_{i+1/2}$）来构建一个四次多项式（获得参数，5个未知数，5个方程）。

from sympy import *
init_printing() # 更好的打印
# 四次多项式
x, y = symbols('x y', real=true)
a1, a2, a3, a4, a5 = symbols('a1:6') # 参数
f = a1*x**4 + a2*x**3 + a3*x**2  + a4*x + a5 - y
# 线性方程: 已知5个点，确定多项式的参数
dx = symbols('dx') #
x3 = symbols('x_3') # 中心边界点的位置
y3 = symbols('y_3') # 中心边界点处C的值
c1, c2, c3, c4 = symbols('c1:5') # 网格平均浓度
# 方程组
f1 = f.subs([(x, x3 - 2*dx), (y, y3 - c1*dx - c2*dx)])
f2 = f.subs([(x, x3 -   dx), (y, y3         - c2*dx)])
f3 = f.subs([(x, x3       ), (y, y3                )])
f4 = f.subs([(x, x3 +   dx), (y, y3         + c3*dx)])
f5 = f.subs([(x, x3 + 2*dx), (y, y3 - c4*dx + c3*dx)])
# 解线性方程组
args = linsolve([f1, f2, f3, f4, f5], [a1, a2, a3, a4, a5])

# 带入多项式
a1, a2, a3, a4, a5 = tuple(*args)
f = a1*x**4 + a2*x**3 + a3*x**2  + a4*x + a5 - y

df = Derivative(f, x).doit()
simplify(df.subs(x, x3))

通过代数求解，可以获得

$$c_{x_{i+1/2}}=\frac{dC}{dx}|x=x_{i+1/2} = \frac{7}{12}(c_i + c_{i+1}) - \frac{1}{12}(c_{i-1} + c_{i+2}) \tag {2.7} \label {2.7}$$

通过该公式，基于网格平均浓度即可计算边界处浓度的值。理论上基于以上公式，就可以进行通量计算了。

对于公式\ref{2.7} ，需要稍加整理。

$$\begin{align*} c_{x_{i+1/2}} &= 0.5(c_{i+1}+c_i) + \frac{1}{6}(\delta c_{i} - \delta c_{i+1}) \\ &= c_i + 0.5(c_{i+1}-c_i) + \frac{1}{6}(\delta c_{i} - \delta c_{i+1}) \\ &\simeq c_i + 0.5(c_{i+1}-c_i) + \frac{1}{6}(\delta_m c_{i} - \delta_m c_{i+1}) \tag {2.8} \label {2.8} \end{align*}$$

其中$\delta c_{i} = 0.5(c_{i+1} - c_{i-1})$ 为第$i$ 个格子的平均斜率（三个网格连续变化的斜率？）。

为了让浓度不连续的地方模拟得更好（steeper representation），同时保证了边界浓度在两个格子平均浓度之间（条件1，不人为创造极值，比如可能出现负数），用$\delta_m c_{i}$ 来替换 $\delta c_{i}$ 。 $$\delta_m c_{i} = \begin{cases} min(|\delta c_{i}|, 2|c_{i+1} - c_{i}|, 2|c_{i} - c_{i-1}|)*sign(\delta c_{i}) &\quad {\text{if } (c_{i+1} - c_{i})(c_{i} - c_{i-1}) \gt 0 }\\ \text{0,} &\quad \text{else} \\ \end{cases} \tag {2.9} \label {2.9}$$

该替换标准是如何获得的呢？

我们把$c_{x_{i+1/2}}$ 的约束条件（浓度值在左右两个格子的平均值之间）带入公式\ref{2.8}，可以得到一个约束$|\delta c_{i}-\delta c_{i+1}|<6|c_{i+1}-c_{i}|$。

更强的一个约束是 $|\delta c_{i}|+|\delta c_{i+1}|<6|c_{i+1}-c_{i}|$，那么如果$|\delta c_{i}|<|3|c_{i+1}-c_{i}|$，且$|\delta c_{i+1}|<|3|c_{i}-c_{i-1}|$，约束条件一定会被满足（为什么PPM的条件会更强一些？）。

注意，替换之后，网格按照$c_{x}$ 积分计算的平均值就与给定的平均值不相等了（不需要一定相等，而且也破坏了边界处的连续性）。

为了避免在间断处出现非物理的振荡（过冲和欠冲，出现这种情况，通量的计算就会变得比较极端，不知道是对是错），在PPM方案中，还有一个约束条件，在一个网格内，浓度的分布是单调的，避免人造极值，破坏物理的合理性，比如负数（网格平均浓度很低，边界浓度差异很大，为了保持抛物线的形态，并且平均值固定，那么就可能出现负值）。

按照之前的公式，得到的$c_{x}$ 不一定在$c_{x_{i-1/2}}$ 和 $c_{x_{i+1/2}}$之间。

• 情况1: 关注格子的浓度$c_{x_{i}}$ 本身就是局地极值。插值函数设置为常数（就是在格子$i$ 中浓度均为$c_{x_{i}}$）。

• 情况2: 格子$i$ 位于浓度梯度很大的地方，比如左边界比右边界浓度大很多，但是该格子的平均浓度与左边界接近，那么二次多项式的曲线会形成比边界浓度更大的值（为了抵消右边比平均值低很多的情况），破坏了在一个格子里面的单调性。这种现象被称为overshoot（过充，或者超调，是指信号或者函数超过了预期值），发生overshoot时，网格左边界和右边界的值就会被重新设定，其判定条件为$|\Delta c_i| < |c_{6,i}|$，该条件通过对公式\ref{2.4} 求导，判定恒大于0 或者恒小于0 得到。

$$\begin{align*} c_{x_{i-1/2}} &= c_{x_{i+1/2}} = c_{i} \quad \text{if } (c_{x_{i+1/2}}-c_{i}) (c_{i}-c_{x_{i-1/2}}) \le 0 \\ c_{x_{i-1/2}} &= 3c_{i} - 2c_{x_{i+1/2}} \quad \text{if } \Delta c_i c_{6,i} > (\Delta c_i)^2 \\ c_{x_{i+1/2}} &= 3c_{i} - 2c_{x_{i-1/2}} \quad \text{if } - \Delta c_i c_{6,i} > (\Delta c_i)^2 \tag {2.10} \label {2.10} \end{align*}$$

其中，$c_{6,i} > 0$ 时，$c(x)$ 为凸函数， $c_{6,i} < 0$ 时，$c(x)$ 为凹函数函数， $c_{6,i} = 0$ 时，$c(x)$ 为线性函数，

$c_{6,i}$ 与 $\Delta c_i$ 同符号时，且判定条件满足，$c_{i}$ 更靠近右边界浓度值。按照$c_{6,i}=\Delta c_i$，带入公式定义公式，求得左边界值，这时在$x_{i+1/2}$ 处(右边界)，$c(x)$ 的导数为0。

$c_{6,i}$ 与 $\Delta c_i$ 符号相反时，且判定条件满足，$c_{i}$ 更靠近左边界浓度值。按照$c_{6,i}=-\Delta c_i$，带入公式定义公式，求得右边界值，这是在$x_{i-1/2}$ 处(左边界)，$c(x)$ 的导数为0

想象一下，如此处理之后，$c(x)$ 在该网格中表现为抛物线的极值 连接边界处。

注意通过该步骤进行替换之后，会破坏边界处的连续性，也就是左右极值不相等（似乎边界处的连续性不是很重要？）!

得到每个网格边界处的浓度值，就能较为容易地计算网格边界处的通量。在边界处传输的平均浓度为

$$\begin{align*} c_{i+1/2, L}(y) &= \frac{1}{y} \int_{x_{i+1/2}-y}^{x_{i+1/2}}c(x)dx \\ c_{i+1/2, R}(y) &= \frac{1}{y} \int_{x_{i+1/2}}^{x_{i+1/2}+y}c(x)dx \tag {2.11} \label {2.11} \end{align*}$$

其中$y$ 假设为正数，表示$c(x)$ 在一次积分时间中，在空间上移动的距离（$y=|u\Delta t|$）。

将公式\ref{2.4} 带入，可以得到

$$\begin{align*} c_{i+1/2, L}(y) &= c_{x_{i+1/2}} - \frac{y}{2\Delta x} (c_{x_{i+1/2}} - c_{x_{i-1/2}} -(1-\frac{2y}{3\Delta x})c_{6,i}) \\ c_{i+1/2, R}(y) &= c_{x_{i+1-1/2}} - \frac{y}{2\Delta x} (c_{x_{i+1+1/2}} - c_{x_{i+1-1/2}} -(1-\frac{2y}{3\Delta x})c_{6,i+1}) \tag {2.12} \label {2.12} \end{align*}$$

对于第$i$ 个格子，公式中的浓度变化代表了从右边传出（$i$ 损失浓度），或者从右边传入的量（$i$ 损失浓度），二者只有一种可能，这取决于风的方向。

from sympy import *
init_printing()
ci = symbols("c_i")
cLi = symbols("cL_i")
cRi = symbols("cR_i")

x = symbols("x")
xLi = symbols("xL_i")
xRi = symbols("xR_i")

dx = symbols("dx")
c6i = symbols("c6_i")

y = symbols("y")

f = cLi + (x-xLi)/dx*(cRi-cLi+(xRi-x)/dx*c6i ) # 公式2.4
fR = integrate(f, (x, xRi-y, xRi))/y # 在边界处进行积分
# 对积分后和方程进行整理
ff = simplify(factor(simplify(fR)).subs(xRi, xLi+dx))
ff.subs(y, dx*x)

在每个网格边界处的单位时间的平均浓度之后，针对某个网格，考虑左右边界的通量，并对时间进行积分，最终就可以获得平流的影响。

$$c_i^{n+1} = c_i^{n} + \frac{\Delta t}{\Delta x}(f_{i-1/2}-f_{i+1/2}) \tag {2.13} \label {2.13}$$ 其中$f_{i+1/2}$ 为边界处的通量。 $$f_{i+1/2} = \begin{cases} u_{x_{i+1/2}} \times c_{i+1/2, L} &\quad {\text{if } u_{x_{i+1/2}} \ge 0 }\\ u_{x_{i+1/2}} \times c_{i+1/2, R} &\quad {\text{if } u_{x_{i+1/2}} \le 0 } \\ \end{cases} \tag {2.14} \label {2.14}$$

PPM的程序实现用到的公式包括:

• 公式 \ref{2.5}
• 公式 \ref{2.8}
• 公式 \ref{2.9}
• 公式 \ref{2.10}
• 公式 \ref{2.12}
• 公式 \ref{2.13}
• 公式 \ref{2.14}