欢迎来到我的知识整理平台!
在大脑中,知识就像存储在硬盘中的数据。只有具备良好的结构,才能方便后续的增删改查。
从无序到有序的转变是一个熵减的过程,虽然常常伴随着一些痛苦,但正是这一过程,让我们逐渐建立起严谨的认知体系。
在这里,我希望通过记录并整理我所学习、思考和探索的知识,并践行费曼学习法,不断推动自己将复杂的知识结构化。
什么是知识
知识是经验和模型综合体。每个人都具备知识,只是有些人经验多,有些人脑子中的模型多。
经验就是每个人看过、听过、触摸过、感受过的对象,是一种记忆。
模型是由概念与概念之间的关系构成的。
概念源自于我们对感觉材料的抽象,而它们之间的关系则包括包含关系、组合关系、因果关系等。
随着现代科学的发展,我们拥有了更先进的观察手段,比如显微镜、光谱分析等,它们极大地延伸了我们的感知能力。 这种感知的增强,让我们观察得更精准,所抽象出来的概念也就更具体、更细致。
与此同时,数理逻辑为我们提供了一种精确的语言,帮助我们准确无误地描述概念之间的关系,使得模型的表达更加严谨。
从本质上说,模型是一种理念中的认知结构,而经验则是现实中感知到的具体体验。
如果理论模型没有任何经验的支持,那它就显得空洞和飘渺;而如果经验缺乏理论的支撑,那它往往是零散而模糊的。
比如我们可能知道“饭怎么做会更好吃”或“沟通怎样更高效”,但这种知识往往是模糊感性的;一旦有人建立了相关的模型(比如烹饪化学、非暴力沟通理论),经验就有了可以归纳和传播的框架。
因此,掌握知识(或学习知识)更多是指对模型的习得。
如何获得知识
经验每个人都在不断获得,虽然机会因人而异,但它们是生活自然产生的;而模型的习得,则需要主动地构建模型与经验的桥梁。
这个桥梁至关重要。
如果一个模型从未用于解释或组织过自身的经验,那么你其实就没有真正掌握这个知识,它只是你大脑中的一个陌生符号罢了。
习得模型之后,我们能够发现经验背后深刻的问题,描述经验背后的模型,能用模型去解释经验的现象,能用模型去预测哪些尚未经验到的个例。
比如,动量守恒定律阐明的是:在一个封闭系统中,系统的总动量是守恒的,这是一个经典的物理理论模型。
在台球桌上,如果一个有初速度的白球撞上了9号球,接下来两个球会分别朝某些方向移动。如果我们掌握了动量守恒的认知模型,就能意识到:这不是随机发生的,而是两个球的动量在相互传递与分配。
通过观察它们的碰撞角度,我们甚至可以解释为什么两个球分别朝那个特定的方向运动。
于是,当我们在看斯诺克比赛直播时,也能大致从选手的出杆姿势和角度判断他的意图,比如是想推进红球,还是想留下母球防守。这种预测能力带来了某种理论上的理解与慰藉,虽然这种慰藉在现实生活中并没什么直接用处,但我们确实感受到:我们明白了。
如果能自然而言地把模型和经验联系起来,我们必然有对知识的掌控感觉。
某方面的专家面对这个领域的现象时,脑子中一定能比这个领域中的小白浮现更多的细节,这就是专家看门道,外行看热闹。
在面对未发生的事情的时候,我们往往可以运用我们过去的经验,或者已习得的模型,进行一定的预测,去指导我们的行为,比如投资的时候用到的各种价值评价模型。
当然,模型本身也存在抽象层级的高低,也就存在普适性强弱的问题。
最基础、最简单的知识掌握方式,其实就是头脑中存储了大量未经加工的经验。这些经验没有经过抽象、没有被系统整理,而只是通过一种模糊的相似性判断来做出预测或解释。
比如,我们的祖先观察到:天上乌云密布时,很可能会下雨;某段时间天气变冷,之后又会变热,人们便形成了对四季循环的模糊认知,进而制定出农历,来指导农业活动。
但这种认知层次,是相对低级的经验性归纳,很多动物其实也具备类似能力。比如我家附近的鸟,每年到了樱桃快熟的季节,就早早守在树上。一旦看到有一颗樱桃红了,它们立刻会飞过去吃掉。它们并没有“模型”,但凭借模糊经验,也能精准把握时机。
作为高级智慧生命,我们真正的智慧在于抽象的能力。我们能够从有限的经验中总结出一般性的模式(归纳),构建出超越具体场景的模型。
这种抽象,并不是简单的经验堆积,而是能够创造出脱离具体经验、但蕴含更广泛意义的符号体系。通过这些符号,我们试图描述事物间的关系,构建出具有更强普适性的认知模型。
当然,这些模型并不等同于宇宙的终极真理,就像牛顿力学在更广阔尺度下被相对论所替代一样。我们构建的模型,只是当前经验的最佳解释,并具有一定的预测能力,但仍可能在面对黑天鹅事件时失效。
尽管如此,现代工业文明和信息文明的快速发展反复证明:基于抽象建模的这条路径,是人类目前最有效的认知方式之一。这些模型一旦系统化,并在实践中被大量经验反复验证,就会发展成一套完整的理论体系,也就是我们今天所说的学科,如物理、化学、经济学等。
然而,我们大多数人接触知识,是从学校开始的。那时我们直接面对的就是学科,从一开始就接触理论模型。这个过程中,虽然我们在不断练习抽象的能力,但却缺乏模型与真实经验之间的连接。
于是,我们学到的知识往往只是书本上的东西,无法与生活产生联系,也难以建立起对知识的掌控感。
如果我们想要对知识产生一种真正的掌控感,最终还是要回到日常生活本身。
我们需要为身边的现象,建立起足够多的认知模型;在日常的观察中,敏锐地找到那些可解释、可映射的模型,并让这些模型反过来对我们的行为产生有意义的指导。
同样地,当我们学习那些纯粹抽象的理论模型时,也应尽可能地寻找与之对应的真实案例,将其与我们熟悉的经验建立联系。这正是我们构建模型与经验的桥梁的过程。
这个过程,其实就是知行合一。
知与行是认知的两面,一体而不可分。我们正是通过在知与行之间的不断往复,逐步把握这个复杂世界的运行逻辑。
当然,这个过程是迭代的:从经验出发,经由抽象建模,再回到实践,再提升抽象……
一圈一圈螺旋上升,直到我们真正建立起对知识的掌控感,以及对生活的把控力。
分享他们
而当我们终于掌握了某些知识之后,下一步就是表达与分享: 我们将脑海中的模型清晰地概括出来,配以生动真实的经验,塑造出有骨有肉、有情有义的知识形态,使抽象与具体交织,激发出深刻而鲜活的认知力。
这些被我们塑造出的知识,最终会通过文本、语音、视频等多种形式被传递出去,去启发他人、照亮他人。
这也许正是我们作为智慧生命,在这个世界上最有价值的行为之一。
数学知识
如果将理性思考视为一种方法论,我会将其定义为精确地观察,精准地描述。即,精确地观察事物的属性,并精准地描述这些属性及其相互关系。而在所有语言中,数学无疑是最能准确表达这些关系的工具——数学是理性思维的语言。
然而,数学的发展早已超越了对具体属性的描述,逐步走向更高层次的抽象。这种抽象并非仅仅是智力游戏,而是通过屏蔽复杂世界的细节,使我们能够直达事物关系的本质。经过抽象后的数学结论,往往能帮助我们洞察事物的本质,而这种洞察,在不借助数学工具的情况下几乎无法获得。
在日常工作中,我接触到的数学知识主要涵盖代数、分析、几何和概率四大分支。每个分支都有独立且漫长的学习路径,例如代数从高等代数到抽象代数,再到李代数。同时,不同分支之间也会相互渗透,形成新的认知体系和工具,例如解析几何、代数几何等交叉领域。
面对日益庞大的数学知识体系,唯有日拱一卒。开始,终究比不开始更好。
代数
解方程是古代代数的核心问题。
在分析客观世界的数量关系时(例如鸡兔同笼问题),用字母表示未知量(代数的字面意思),并通过等量关系(数值相等)列出方程(运算)。随后,利用运算律和等量公理(自反性、对称性、传递性、替换性)求解方程。
脱离解方程的目的,如果从更抽象、更全局的角度来看研究对象,涉及以下几个关键要素:
-
集合:数量取值的范围(如自然数)。
-
运算:集合到集合映射(比如二元运算),定义在该集合上的运算(如加法、乘法)。
-
运算在集合上应该满足的性质:如封闭性、可逆性、结合律等。
定义(找到)集合,并在其上赋予运算及运算必须满足的性质,就形成了一个代数体系(Algebraic Structures),比如群、环、域、n 维向量空间。 不同的代数体系对运算及其性质的要求各不相同。
1. 群(Group) 定义:一个群 \( (G, \cdot) \) 是一个集合 \( G \) 与一个二元运算 \( \cdot \) 组成的代数结构(运算只是一种记号,可以是仍和的运算),满足以下公理:
- 闭合性(Closure):对于所有 \( a, b \in G \),\( a \cdot b \in G \)。
- 结合律(Associativity):\( (a \cdot b) \cdot c = a \cdot (b \cdot c) \)。
- 单位元(幺元,Identity):存在一个元素 \( e \in G \),使得对所有 \( a \in G \) 有 \( e \cdot a = a \cdot e = a \)。
- 逆元(Inverse):对于每个 \( a \in G \),存在 \( a^{-1} \in G \),使得 \( a \cdot a^{-1} = a^{-1} \cdot a = e \)。
特殊情况:
- 具备前两个性质,则称为半群
- 具备前三个性质,则成为幺半群
- 若还满足交换律(Commutativity):\( a \cdot b = b \cdot a \),则称为阿贝尔群(Abelian Group)。
2. 环(Ring) 定义:一个环 \( (R, +, \cdot) \) 是一个集合 \( R \) 配备了两个运算 \( + \) 和 \( \cdot \),满足:
- \( (R, +) \) 是阿贝尔群。
- \( (R, \cdot) \) 是一个半群。
- 分配律:\( a \cdot (b + c) = a \cdot b + a \cdot c \) 且 \( (a + b) \cdot c = a \cdot c + b \cdot c \)。
特殊情况:
- 若 \( (R, \cdot) \) 满足交换律,则称 \( R \) 为交换环(Commutative Ring)。
- 若 \( (R, \cdot) \) 是一个幺半群,则称为含幺环(Ring with Unity)。
3. 域(Field) 定义:一个域 \( (F, +, \cdot) \) 是一个特殊的环,它同时满足:
- \( (F \setminus {0}, \cdot) \) 是阿贝尔群。
例子:有理数域 \( \mathbb{Q} \)、实数域 \( \mathbb{R} \)、复数域 \( \mathbb{C} \)
4. 线性空间(Vector Space) 定义:一个线性空间 \( V \) 是在一个域 \( F \) 上的阿贝尔群,并配备一个数乘运算 \( \cdot: F \times V \to V \),使得:
- 封闭性:\( \alpha v \in V \)(其中 \( \alpha \in F, v \in V \))。
- 对标量的分配律:\( (\alpha + \beta)v = \alpha v + \beta v \)。
- 对向量的分配律:\( \alpha (v + w) = \alpha v + \alpha w \)。
- 数乘结合律:\( (\alpha \beta) v = \alpha (\beta v) \)。
- 单位元作用:\( 1 v = v \)(其中 \( 1 \) 是 \( F \) 的乘法单位元)。
例子:
- 向量空间 \( \mathbb{R}^n \) 是 \( \mathbb{R} \) 上的向量空间。
- 矩阵空间:所有 \( n \times m \) 矩阵构成一个线性空间。
- 多项式空间:所有次数不超过 \( n \) 的多项式构成一个线性空间。
从数学构建的层次关系来看,群是最基本的代数体系,域是相对高级的代数体系, 但是从实际的数学认知来看,我们是现在自然数集合开始认识数以及运算,再到整数集合, 再到遇到第一个对运算封闭的集合,有理数域,直到实数域。最后在解方程(多元一次方程组,一元高次方程)的过程中,为了回答解的存在和结构问题,定义了代数体系,反过来又用代数体系重新审视了基础代数的基本定义。
代数体系的构建远不止用于解方程。例如,可以通过群论研究对称性,用环论分析非对称加密问题等。
近现代代数的核心问题在于研究代数体系的内部结构及其同态映射,揭示不同代数结构之间的联系。
因此,汲取现代代数的思想来审视实际工作中的问题,往往能提供一种独特的视角,帮助我们更深刻地理解问题的本质。
线性代数
只考虑满秩的矩阵。不满秩的矩阵其实是一种信息的冗余,没有太多意义,可以通过去掉一些列,变成满秩的。
- 矩阵用来解释一次线性方程组解的性质(是否存在、如何求解、解的空间、有解的空间),\(Ax = b\),从几何的视角看,就是用 \( A \) 中的列向量作为基,是否能表示 \( b \) ? 可以通过列空间,行空间,零空间去看解的结构,\( x \) 可以 换元,也就是矩阵乘法,可以用逆矩阵来求解。
- 方阵可以表述坐标线性转换,比如旋转。坐标变换可以叠加,也就是矩阵乘法。对角矩阵的变换只是对原来的基向量的缩放,原来的基向量就是特征向量。对角矩阵是一种最简单的坐标转换(求幂,求逆,求行列式,都很简单,是最好处理的矩阵,对角化之后,还可以把矩阵写成一系列特征值乘以分矩阵的形式,类似基矩阵的感觉,在具体的应用中可以看作谱),也代表了这一类矩阵描述的转换的最简单形式(矩阵的相似性,\( Q \Lambda Q^{-1} \),特征值对角矩阵是一类矩阵最简单的描述),实对称矩阵的特征向量是正交的,正定矩阵的性质比较好(如何确定一个矩阵是正定的?),所有特征值都是正实数,求特征值有一些技巧,和迹的关系,以及和行列式的关系。
- \( Ax \),也可以理解换基,换基可以分为方阵表示的坐标变换和非方阵表示的降维和升维。对于坐标变换而言,矩阵的行列式表示,表换之后面积、体积的缩放尺度。
- 可以对坐标转换进行换基, \( B^{-1}MB \),\( B \) 表示视角的转换, \( M \) 表示坐标转换(我让一支笔顺时针旋转,那么我对面的人,看到的是什么?)。 如果 \( M \) 表示顺时针,那么我们对面的人看到的就是逆时针,\( B^{-1}MB \) 就是一个逆时针变换的矩阵。
- 用矩阵表示投影。利用点积,避免了角度的运算(反三角函数其实很烦人),\( A(A^TA)A^T \),\( M \) 的列数大于行数才有意义。投影从另一个意义上讲,也可以看作一种压缩。 用 A 中的列表示 \( b \) 向量时,有些列的贡献可能很小(有损压缩,也就是投影),有些列可能为 0(无损压缩,说明找到的基很好),向量的点积代表了向量的空间垂直关系,本身也可以看作一种投影,但是是投影在向量上,而不是向量坐在的空间上。
- A 的行数大于列数时,对矩阵与向量的乘法,算是升维(本质也是换基),把一个二维的向量,变成三维的有什么意义? 原来的二维向量,只是某个三维空间中的面(注意二维向量是任意的,在三维空间中,二维向量在三维基向量上可以都有值,这其实才是普遍现象),升三维之后,能有另一个维度的信息表示能力,或者说从其他角度去看待同一个东西(本来二维可以唯一确定一类东西,但是我们希望从其他角度来看待,能帮助我们看到二维遮蔽的信息)。
- SVD 是方阵对角化的非方阵推广,\( U \Sigma V^{T} \))。
- PCA,找到投影后的数据方差最大的基(这些方向,主导了数据的变化)。\( (\frac{1}{n} X^T X) w = \lambda w \)),基就协方差矩阵的特征向量,也能实现数据压缩的目标,同时可以作为一种分析工具,表明主要矛盾在那些方向。
- 离散傅里叶变换中的矩阵可以表示为 \( F_{ij} = w^{i+j}\) 其中, \( w^n = 1\),一般用复指数的方式表示 \( w = e^{i2\pi/n}\),该矩阵为 复 Hermitian 矩阵,很容易得到逆矩阵,从而进行离散傅里叶变换的逆变换。
线性映射
在两个向量空间之间的映射 \( T: V \to W \) 被称为线性映射(Linear Map)或线性变换(Linear Transformation),如果它满足以下两个条件,对任意 \( \mathbf{u}, \mathbf{v} \in V \) 和标量 \( a \in \mathbb{F} \):
-
加法保持性(Additivity): \[ T(\mathbf{u} + \mathbf{v}) = T(\mathbf{u}) + T(\mathbf{v}) \]
-
数乘保持性(Homogeneity): \[ T(a \mathbf{u}) = a T(\mathbf{u}) \]
即,线性映射保持向量加法和数乘运算。
等价定义
线性映射 \( T: V \to W \) 可以等价地表示为: \[ T(a \mathbf{u} + b \mathbf{v}) = a T(\mathbf{u}) + b T(\mathbf{v}), \quad \forall \mathbf{u}, \mathbf{v} \in V, \forall a, b \in \mathbb{F} \] 即,线性映射保持线性组合的运算。
特殊情况
- 如果 \( V = W \),则 \( T \) 是从自身到自身的线性变换(线性算子,有时候一个意思,有时候有所区分)。
- 如果 \( T \) 映射到数域 \( \mathbb{F} \)(即 \( W = \mathbb{F} \)),则 \( T \) 是一个线性函数(比如 多元一次函数)。
矩阵表示
如果 \( V \) 和 \( W \) 都是有限维向量空间,则线性映射可以用矩阵 \( A \) 表示(不能有高次,最后就写到了多元一次函数方程组): \[ T(\mathbf{x}) = A \mathbf{x} \] 其中,\( A \) 是一个 \( m \times n \) 矩阵,\( \mathbf{x} \) 是 \( n \) 维列向量,\( T(\mathbf{x}) \) 是 \( m \) 维列向量。
例子
-
简单的数乘变换: \( T: \mathbb{R}^2 \to \mathbb{R}^2 \),定义为 \( T(x, y) = (2x, 3y) \),满足线性性,因此是线性映射。
-
矩阵变换: 设 \( A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix} \),则映射 \( T(\mathbf{x}) = A \mathbf{x} \) 是线性映射。
-
积分算子: 设 \( V \) 是所有连续函数的空间,定义 \( T(f) = \int_0^x f(t) , dt \),可以验证 \( T \) 也是线性映射。
几何
拓扑学
分析
广延量与强度量:数学与物理世界的桥梁
广延量与强度量
在物理学和数学的世界里,我们常将量分为两类:
- 广延量(测度):体积、时间、质量、能量、电荷、熵 等等。
- 强度量(可测函数):密度、浓度、速度、温度、压强、效率 等等。
守恒定律都是建立在广延量上的,广延量才是更基本的量。强度量则往往是我们在研究广延量变化时引入的中间变量或工具。
为了方便广延量之间的转换(例如通过时间得到距离,通过体积得到质量)以及进行维度的提升(例如从长度求面积,从面积求体积),我们创造了复杂的数学工具体系。
数学抽象与现实世界
现实物理世界中,人能够感知到的物理实体都是具有三维体积的。我们用解析几何的方法,通过建立笛卡尔坐标系,试图准确描述对象的位置信息。
然而,点、线、面这些在笛卡尔坐标系中抽象出来的数学概念,在现实世界中是不存在的。但“点”这一概念是多么迷人,多么纯粹而干净。
为了获得“点”这种抽象,我们必须对空间进行无限分割。但我们真的理解“无限分割”吗?在这个过程中,我们一步一步定义出了实数域这样一个抽象而复杂的数学结构。
实数域中的每一个无理数,其实都包含了无穷多的信息。曾有科幻小说提出一个设想:将现有所有信息用数字编码成一个\(0.abcsdfsf\ldots\)这种形式的小于1的无理数,然后以这个无理数的长度切割一根单位长度的木棍,就能记录所有信息。只要能够准确测量这根短棍的长度,我们便可以获得所有信息。当然,现实世界中的测量必然受到物理极限的制约,这使得这种以一个无理数编码所有信息的设想只存在于理论与科幻之中(我们永远没办法精确的到,无理数其实在实际应用中没有太多意义)。
常人很难想象实数域的结构是什么。一个无理数我们都无法完全表象出来,更难以想象任意两个数之间永远存在无穷多个数的感觉。这本来就是“在现象上不存在”的概念。
函数、导数和积分
在实数域的基础上,为了描述量之间的关系,我们引入了映射(函数)的概念。
函数的定义是建立在“点”的基础上的。但点上有什么?点上没有体积,没有质量。但是,我们可以在点上定义强度量——如密度、速度。
强度量本身无法直接观测,只能通过广延量之比得到:
\[ \text{密度} = \frac{\text{质量}}{\text{体积}} \]
要得到“点上的量”,我们就必须通过极限与导数,将广延量(测度)转化为强度量(可测函数)。
而导数的逆过程就是积分,通过积分可以完成从一个测度到另一个测度的转换,即:从点上的属性(如密度)反推到具有空间尺寸的量(如质量)
点之所以能在积分中发挥作用,正是因为我们赋予了它强度量的属性,从而通过积分的方式重新获得广延量。
为了保证整个过程的严谨性,我们发展出了\(\varepsilon\)-语言,并引入连续、可导、可测、可积等概念。借助积分与导数,我们得以在不同维度和测度之间来回跳跃。
相关数学关系
- \(\text{广延量} \times \text{广延量} = \text{广延量}\)(维度提升)
- \(\text{广延量} \div \text{广延量} = \text{强度量}\)
- \(\text{广延量} \times \text{强度量} = \text{广延量}\)
- \(\text{强度量} \times \text{强度量} = \text{强度量}\)
当然,在数学意义上,强度量与广延量的界限,并非绝对,而是建立在所选测度体系之上的相对关系(高阶导数,比如加速度和速度)。
强度量是手段,广延量是目的
通常来说,强度量只是我们的手段,广延量才是我们的目的。例如我们提升速度与效率,都是为了节约更重要的广延量:
- 节约时间(生命的长度)
- 节约能量(资源的总量)
- 节约质量(材料的用量)
我们所追求的效率提升,归根结底是为了优化广延量的消耗。因此,强度量不过是通往广延量的桥梁。
强度量不过是数学世界架起通向广延量的桥梁,而广延量则是我们在现实世界中真正能够触碰到的存在。
变分法
物质导数
在流体力学研究中,我们通常关心流体中的物理量(如密度 ( \rho )、速度 (\mathbf{v})、温度 (T) 等) 如何随时间和空间变化。为了描述随流体运动的某一点的性质变化, 我们引入物质导数(Material Derivative)。
物质导数是沟通拉格朗日法和欧拉法的核心公式。 拉格朗日法关注的是随流线移动的流体微元内部的属性。 欧拉法关注的是三维空间中固定位置的微元内部的属性。
物质导数是沿着流线的变化率(全导数)。
流线是关于时间的函数(关于时间的参数方程)。 [\mathbf{x} = \mathbf{x}(t)]
随着流线移动的微元的属性可以表示为 [\rho = \rho(\mathbf{x}(t), t) ]
物质导数就是对随流线移动的流体微元的属性求时间的导数, 根据多元函数的微分法则可知。
[ \frac{D \rho}{ D t} = \frac{\partial \rho}{\partial t} + \frac{\partial \rho}{\partial \mathbf{x}} \frac{\partial \mathbf{x}}{\partial t} = \frac{\partial \rho}{\partial t} + \mathbf{v} \cdot \frac{\partial \rho}{\partial \mathbf{x}} ]
要理解该公式,首先要注意, 随流线移动的流体微元 是一个随时间移动的立方体 (一个纯粹的几何体,可以是其他形状的微元,但是必须是微分体积), 当时间固定时,随流线移动的流体微元 会与 一个 三维空间中固定位置的微元 重合。

微元并不是包含流体的一个流体团(只是一个形状不变的几何体),因此,其体积内部并不是质量守恒的。 随流线移动的流体微元 内部的属性随时间的变化(比如密度) 包含两个部分,一部分是与当前随流线移动的流体微元重合的 三维空间中固定位置的微元的属性变化 (没有源汇的情况,微元表面的通量导致局部变化)。 另一部分是微元随着流线移动一小步(微元的位置会随时间变化)导致的变化。
[ \frac{D \rho}{ D t} = \frac{\rho_{t+\Delta t}^{trace} - \rho_{t}^{trace}}{\Delta t} ] 其中,$\rho^{trace}$ 是指随流线移动的流体微元的密度 [ \frac{\partial \rho}{\partial t} = \frac{\rho_{t+\Delta t}^{local} - \rho_{t}^{local}}{\Delta t} ] 其中,(\rho^{local}) 是三维空间中固定位置的微元的密度
注意,在 (t) 时刻,随流线移动的流体微元与三维空间中固定位置的微元 重合。 因此 (\rho_{t}^{trace} = \rho_{t}^{local}) [ \frac{D \rho}{ D t} - \frac{\partial \rho}{\partial t} = \frac{\rho_{t+\Delta t}^{trace} - \rho_{t+\Delta t}^{local}}{\Delta t} ]
在 (t+\Delta t) 时刻,随流线移动的流体微元与三维空间中固定位置的微元 不重合。 存在偏移, 偏移量与流体微元在 (t) 到 (t + \Delta t) 时刻的速度相关
[ \rho_{t+\Delta t}^{trace} - \rho_{t+\Delta t}^{local} = \frac{\int\limits_{t}^{t+\Delta t} v(t), dt}{\Delta x} (\rho_{t+\Delta t}^{local+\Delta x} - \rho_{t+\Delta t}^{local}) ]
根据积分中值定理, 由于 (\Delta t \to 0) [ \int\limits_{t}^{t+\Delta t} v(t), dt \approx v_t \Delta t ]
因此 [ \frac{\rho_{t+\Delta t}^{trace} - \rho_{t+\Delta t}^{local}}{\Delta t} = v_t \frac{\rho_{t+\Delta t}^{local+\Delta x} - \rho_{t+\Delta t}^{local}}{\Delta x} = v_t \frac{\partial \rho}{\partial x}|_{t=t+\Delta t} ]
可得 [ \frac{D \rho}{ D t} = \frac{\partial \rho}{\partial t} + v_t \frac{\partial \rho}{\partial x}|_{t=t+\Delta t} ]
根据泰勒展开,且 (\Delta t \to 0),最后可得一维的情况 [ \frac{D \rho}{ D t} = \frac{\partial \rho}{\partial t} + v \frac{\partial \rho}{\partial x} ]
物质导数的意义
可以根据物质导数定义一些特殊的流体,比如可以给出不可压缩流体的定义为 [ \frac{D \rho}{ D t} = 0 ] 如果是一维情况,不可压缩流体意味着流体本身运动与微元的运动是一致的。
根据连续性方程, [ \frac{D \rho}{ D t} = - \rho \nabla \cdot \mathbf{v} = 0 ]
不可压缩流体并不意味着流体性质均一,因此 (\rho \neq 0), 所以可得 [ \nabla \cdot \mathbf{v} = 0 ]
如果只看二维的情况 [ \nabla \cdot \mathbf{v} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 ] 也就意味着在 $x$ 方向的压缩,会导致在 $y$ 方向膨胀。
同时物质导数直观的反映了沿着流线的属性变化, 比如一根流线分别在三点和四点经过的苏州上海。 苏州三点温度为 20 度,上海四点维度为 21 度。 可以认为 20 度是温度平流, 而多出来的 1 度是气团在流动过程中被加热了(热传导、做工、热辐射等)
概率
研究客观世界中的不确定现象(随机现象)。
如何研究?
对于某个不确定现象,我们可以通过建模选定一个样本空间 \(\Omega\),并在其上构造一个 \(\sigma\)-代数 \(\mathcal{F}\),从而形成可定义事件的结构。进一步引入一个概率测度 \(\mathbb{P}\),使得三元组\((\Omega, \mathcal{F}, \mathbb{P})\) 成为一个概率空间。 在此基础上,我们可以定义从 \(\Omega\) 到其他测度空间(例如实数集 \(\mathbb{R}\) 及其 Borel \(\sigma\)-代数 \(\mathcal{B}(\mathbb{R})\))的可测函数,称为随机变量(同一个概率空间可以定义多个不一样的随机变量)。即 \[ X : \Omega \to \mathcal{B} \] 满足对任意 Borel 集合 \(B \in \mathcal{B}(\mathbb{R})\),有 \[ X^{-1}(B) = {\omega \in \Omega : X(\omega) \in B} \in \mathcal{F}. \]
每个随机变量在概率测度 \(\mathbb{P}\) 下诱导出一个概率分布函数: \[ F_X(x) = \mathbb{P}(X \leq x), \quad x \in \mathbb{R}. \]
该分布函数由随机变量 \(X\) 和概率测度 \(\mathbb{P}\) 联合唯一确定。
有了随机变量的概率分布函数后,我们可以计算其各种统计特性,以及一些收敛性质,例如:
- 期望(数学期望): \[ \mathbb{E}[X] = \int_{-\infty}^{+\infty} x , dF_X(x) \]
若 \(X\) 有概率密度函数 \(f_X(x)\),则写成 \[ \mathbb{E}[X] = \int_{-\infty}^{+\infty} x f_X(x) , dx \]
- 方差: \[ \mathrm{Var}(X) = \mathbb{E}[(X - \mathbb{E}[X])^2] = \int_{-\infty}^{+\infty} (x - \mathbb{E}[X])^2 , dF_X(x) \]
贝叶斯
测度
测度是长度、体积等概念的推广,是回答复杂集合的大小的工具,长度可以理解为某个线段中所有点的组成集合的大小,点本来没有长度,但是无限个点,组成的线段,就有了长度,那么怎么样的无限个点组成的集合才应该有长度呢?长度又是多少呢?(比如所有有理数点组成的集合,所有自然数组成的集合有长度吗?)
测度是自变量为集合,值域为非负的函数。要研究测度,首先要搞清楚集合,也就是搞清楚自变量。
集合和基本运算
集合(Set)是确定的、无序的、互不相同的对象组成的整体。通常记作大写字母表示集合,小写字母表示元素。例如,集合 \(A = \{1,2,3\}\)。
如果元素 \(a\) 属于集合 \(A\),我们写作: \[ a \in A \] 如果元素 \(a\) 不属于集合 \(A\),我们写作: \[ a \notin A \]
集合 \(A\) 与集合 \(B\) 的并集,记作: \[ A \cup B = \{x \mid x \in A \text{ 或 } x \in B\} \]
集合 \(A\) 与集合 \(B\) 的交集,记作: \[ A \cap B = \{x \mid x \in A \text{ 且 } x \in B\} \]
集合 \(A\) 与集合 \(B\) 的差集(或补集),记作: \[ A - B = \{x \mid x \in A \text{ 且 } x \notin B\} \]
集合 \(A\) 和 \(B\) 的对称差,记作: \[ A \Delta B = (A - B) \cup (B - A) \]
集合序列和极限
\( A = \{ A_n, n=1,2,3 ... \} \) 是一个集合序列(集合的集合)。
定义:
- \( \inf A = \bigcap_{n=1}^{\infty} A_n \) 为 集合序列 \( A \) 的下界(所有元素的交集,肯定是最小的集合)。
- \( \sup A = \bigcup_{n=1}^{\infty} A_n \) 为 集合序列 \( A \) 的上界(所有元素的并集,肯定是最大的集合)。
如果 \( A = \{ A_n, n=1,2,3 ... \} \) 中 的集合都满足, \( A_n \subseteq A_{n+1} \),则称该集合序列具有非降属性。可以记作 \( A \uparrow \)。其极限:
\[ \lim_{n \to \infty} A_n = sup A = \bigcup_{n=1}^{\infty} A_n \]
为什么要这么定义? 随着 \( n \) 的增加,\( A_n \) 越来越大,最大的不就是最后一个集合吗? 这样考虑在有效的集合序列中是没有问题的,但是对于无限集合序列不适用,比如 \( A = \{ [1/n, 1], n=1,2,3 ... \} \) ,该集合序列没有最后一个元素,需要用极限的语言来表达他的上界。
同理,如果 \( A = \{ A_n, n=1,2,3 ... \} \) 中 的集合都满足, \( A_n \supseteq A_{n+1} \),则称该集合序列具有非升属性。可以记作 \( A \downarrow \)。其极限:
\[ \lim_{n \to \infty} A_n = inf A = \bigcap_{n=1}^{\infty} A_n \]
也就是在无限远处,存在该集合序列的最小元素集合。
那么对于任何(也就是没有单调的属性)集合序列 \( A = \{ A_n, n=1,2,3 ... \} \),可以构造一个非升 和一个 非降的集合序列 \[ A^{d} = \{ A_n^{d}=\bigcup_{k=n}^{\infty}A_k, n=1,2,3 ... \} \]
\[ A^{u} = \{ A_n^{u}=\bigcap_{k=n}^{\infty}A_k, n=1,2,3 ... \} \]
序列 \( A \) 的上极限定义为 \[ \lim_{n \to \infty} \sup As_n = \lim_{n \to \infty} A_n^{d} = \inf A^{d} = \bigcap_{n=1}^{\infty} A_n^{d} = \bigcap_{n=1}^{\infty} \bigcup_{k=n}^{\infty}A_k \]
其中 \( As_n = \{A_k, k=n,n+1,...\} \)
序列 \( A \) 的下极限定义为 \[ \lim_{n \to \infty} \inf As_n = \lim_{n \to \infty} A_n^{u} = \sup A^{u} = \bigcup_{n=1}^{\infty} A_n^{u} = \bigcup_{n=1}^{\infty} \bigcap_{k=n}^{\infty}A_k \]
- 上极限表示,当 \( n \) 足够大时,经常会出现的元素。
- 下极限表示,当 \( n \) 足够大时,总是会出现的元素
因此,上极限总是比下极限的集合大:
\[ \lim_{n \to \infty} \inf As_n \subseteq \lim_{n \to \infty} \sup As_n \]
当集合序列的上极限和下极限都存在,且相当时,集合序列的极限存在。
集合系
设 \(X\) 为一个集合,\( \mathcal{F} \) 为 \(X\) 的子集的一个集合族,则 \( \mathcal{F} \) 称为 \(X\) 上的一个集合系。
集合系 是一种特殊的 集合序列,其元素集合均是某个集合 \(X\) 的子集。
- \(\pi\) 系:对交运算封闭的非空集合系
- 单调系:单调序列极限封闭的集合系
- \(\lambda\) 系:差运算封闭的 单调系
- 半环:差集可分解成有限并 的 \(\pi\) 系
- 环:并、差运算 封闭的集合系
- 域:对 \(X\) 的差 封闭的 \(\pi\) 系
- \(\sigma\) 域:对可数并封闭的 域
基础的集合系可以生成复杂的集合系,比如 \(R\) 上的素有开集组成的集合系,可以生成一个 \(\sigma\) 域,也被称为 Borel 集合系记作:
\[ B(R) = \sigma(\{ (a,b)| a<b, a,b \in R \} ) \]
\(\sigma\) 域 可以作为测度函数的定义域(保障可数的并/交运算闭合),和\(X\)放在一起,被称作可测空间。
可测函数(可测映射)
设 \((X, \mathcal{F})\) 和 \((Y, \mathcal{G})\) 是可测空间,函数\( f : X \to Y \)称为可测函数(随机变量),如果对于任意 \(B \in \mathcal{G}\), \[f^{-1}(B) := \{x \in X : f(x) \in B\} \in \mathcal{F}\]
通常 \(Y = \mathbb{R}\),\(\mathcal{G}\) 是 Borel \(\sigma\)-代数。
可测函数保证了测度上的结构在函数映射下是可追踪的,即函数的逆像保持在原来的测度空间的可测集合中,从而能定义积分、概率等。
独立随机变量序列
Kolmogorov's Zero-One Law(柯尔莫哥洛夫 零一律)
设 \((\Omega, \mathcal{F}, \mathbb{P})\) 是一个概率空间(测度空间),定义在该概率空间上的无限独立同分布随机变量序列 \(\{ x_n\}_{n=1}^{\infty}\) \[ \{X_n : \Omega \to \mathbb{R}, \quad n = 1,2,3,\dots\} \]
以无限次投掷一枚公平硬币为案例说明符号对应的具体东西,正面用 1 表示,反面用 0 表示,首先是样本空间
\[ \Omega = \{ w_n:w_n=(a_k: a_k \in \{0, 1\}, \quad k=1,2,3,\dots), \quad n=1,2,3,\dots\} \] 也就是说样本空间中的每个元素都是一个 \[ w_n = (a_1, a_2, a_3, \dots) \]
可测集的集合系(事件空间,事件系统,σ-代数) \( \mathcal{F} \) 可以表示为
\[ \mathcal{F} = \sigma(\Omega) \]
这个生成过程,比较复杂,可以先理解为幂级集合系。
对于抛硬币,为正的概率为 \(p=\frac{1}{2}\) 事件空间的测度(概率测度)为
\[ P(A \in \sigma(\Omega) ) = \sum_{w \in A} \Pi_{i=1}^{n} p^{a_i}p^{1-a_i} = \sum_{w \in A} \frac{1}{2^n} \]
可以看出,如果 n 趋近于无穷大,单点事件 \(\{ w_n \} \)的概率为 0 。
我们再在 测度空间 \((\Omega, \mathcal{F}, \mathbb{P})\) 的基础上定义随机变量序列
\[ (X_k: \Omega \to \{0, 1\}; \quad X_k(w)= w[k] = a_k) \] 也就是第 k 次抛硬币出现的情况(这样定义,我们才能获得一个无限同分布的随机变量序列)。
定义 尾 σ-代数(tail σ-algebra)为: \[ \mathcal{T} = \bigcap_{k=1}^\infty \sigma(X_k, X_{K+1}, \dots) = \bigcap_{k=1}^\infty \sigma(X_m: m \geq k) \]
注意是并集,换句话说,\(\mathcal{T}\) 中的事件只与无限远的未来有关,而与任意有限个 \(X_1, X_2, \dots, X_k\) 无关。
如何理解 尾 σ-代数?
最关键的是理解生成过程:
\[ \sigma(X_k, X_{K+1}, \dots) = \sigma({ X_k^{-1}(B_k) \bigcap X_{k+1}^{-1}(B_{k+1}) \dots; B_k \in {0, 1}}) \]
因此 \[ w \in \sigma(X_k, X_{K+1}, \dots) \to w \in \Omega \]
也就是说尾 σ-代数 的样本空间仍然是 \(\Omega\),但是尾 σ-代数中的事件之间的差别只能是远处的无穷项决定。
以无限次投掷一枚公平硬币为案例,我们描述一个事件(注意事件的本质是集合),正反次数出现的频率极限是为 0.5。
\[ A = \{w: w \in \Omega, \lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^{n} X_k = \frac{1}{2}\} \in \mathcal{T} \]
正反次数出现的频率 是和 远处的无限个样本相关的,于过去的样本没有关系。
柯尔莫哥洛夫零一律描述为:
如果 \(\{X_n\}\) 是独立随机变量序列,那么对于所有属于尾 σ-代数 \(\mathcal{T}\) 的事件 \(A\),有: \[ p(A) \in \{0, 1\} \]
由于尾事件与任何有限个 \(X_n\) 无关,因此其概率在给定任何有限信息后都不改变。因此尾事件对所有有限信息都是 条件独立的。
\[ P(A) = P(A|\sigma(X_1,..., X_k) ) \]
根据条件期望的定义(以及概率分布),可以得到: \[ P(A) = E[1_A|\sigma(X_1,..., X_k)] \]
其中 \( 1_A \) 就是简单函数构建的可测函数(随机变量)
对 k 求极限(马氏收敛定理) \[ P(A) = \lim_{k \to \infty } E[1_A|\sigma(X_1,..., X_k)] = 1_A\]
也就是说\( P(A) \in \{0, 1\} \) ,这说明要么 𝐴 几乎必然发生(概率 1),要么几乎必然不发生(概率 0)。
随着你知道的硬币次数越来越多,你的预测会逐渐变得确定,我们观测到正反面几乎各种一半。也就是说,无论我们什么时候抛硬币足够多,都可以得到接近0.5的概率(正反面各占一半的概率是为 1 )
零一律告诉我们,在无限独立实验下,某些问题根本没有不确定性(比如,均值,方差),要么必然发生,要么必然不发生。
大数定律
随着试验次数的增加,样本均值会趋近于总体的数学期望。
样本均值 \(\overline{X}_n\) 以概率收敛到总体期望 \(\mu\),即弱大数定律成立。
\[ \lim_{n \to \infty} P(|\overline{X}_n - \mu| \geq \varepsilon) = 0. \]
样本均值几乎处处收敛到期望 \(\mu\),即强大数定律 \[ P\left( \lim_{n \to \infty} \overline{X}_n = \mu \right) = 1, \]
- 大数定律为频率解释概率提供数学基础。保证了大量重复试验中样本均值会接近理论期望,从而使概率的频率意义成立(指示函数,发生和不发生)。
- 在实际数据分析和统计推断中,利用大数定律可以相信样本均值是总体均值的合理估计,支撑样本均值的可靠性。
- 通过大量随机样本计算平均值,用来估计复杂问题的期望值或概率,是数值计算的重要工具(数值模拟和蒙特卡洛方法)。
物理相关
热力学
熵
扩散
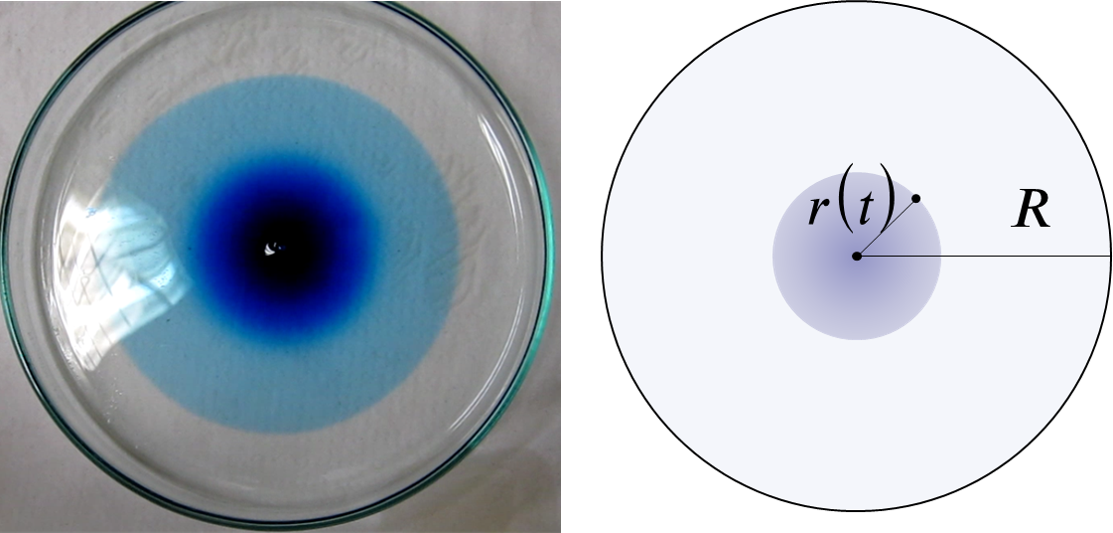
引子
对于流体,其分子不断做不规则的随机运动(热运动),由于分子间的频繁碰撞,这种运动表现出高度的随机性,导致两类宏观现象,对于单个较大的颗粒(如悬浮颗粒),受涨落影响(粒子足够小,不同时间被分子撞击的力并不相等,也就是受力的涨落),发生布朗运动;而对于大量的小分子群体(一滴墨水滴入水中),表现为扩散现象(我们没办法从视觉上看到单个分子的运动轨迹)。
在统计意义上,这些粒子(无论是大颗粒还是小分子)在流体中的随机位移,随着时间的推移,会受到微扰的累计影响。根据中心极限定理,大量独立、微小的随机扰动累加后的分布趋于高斯分布。
因此,它们的位置概率密度满足如下形式的高斯解:
\[ \rho(x, t) = \frac{1}{\sqrt{4\pi Dt}} e^{\frac{-x^2}{4Dt}} \]
我们观察点源的扩散现象,由于大量示踪分子的存在,使得我们能够明显从直觉上感知到高斯分布的存在。而布朗运动的轨迹可以被看作是从概率分布中采样得到的路径(就像量子波函数的坍塌),从一个连续的概率分布中,观测后得到一个确定的结果。
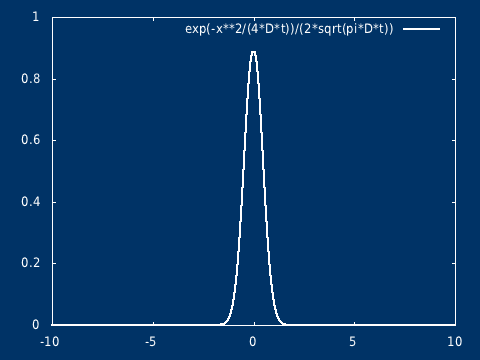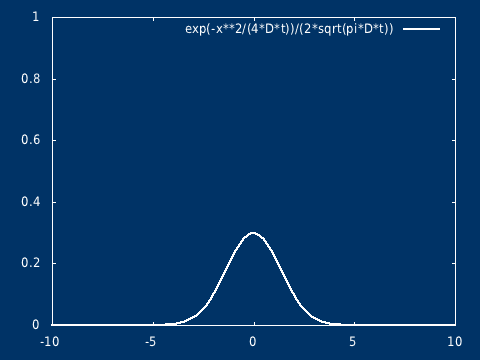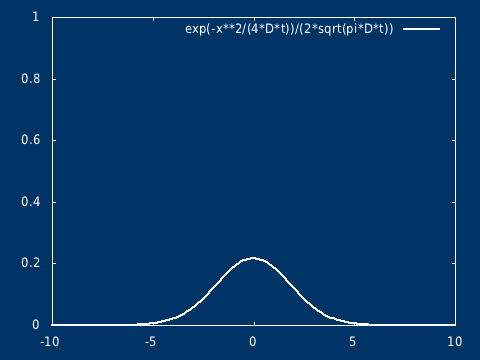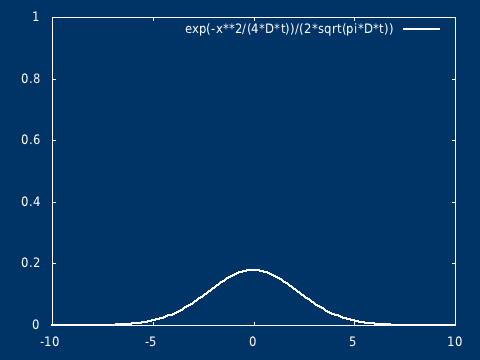
高斯扩散
设在无界空间中,污染物在某一点瞬时释放,总质量为 \( Q \) ,扩散过程(分子扩散)满足 \[\frac{\partial C}{\partial t} = D \nabla^2 C\] \[C(0, x) = Q\delta(0)\]
- \( \delta(0) \) 表示初始时刻在原点释放污染物
- \( D \) 为扩散系数
该方程的解析解为: \[ C(t, x) = \frac{Q}{\sqrt{ 4\pi D t} } \exp( -\frac{ x^2}{4 D t} ) \] \( t=0, x = 0\),浓度无限大,相当于是一个奇点(但是不发散),在初始时刻不再是经典意义下的函数,而是趋于 Dirac δ 函数(高斯分布在标准差趋于 0 的极限下,会趋于 Dirac δ 函数,即 δ 函数是高斯分布族在某种极限意义下的结果)
可以很容易推广到二维(以及三维)。其物理意义,可以想象是在静止的水面(水很浅),点入一滴墨水,墨水向四周扩散,墨水滴入的地方是高值中心,随着时间的推移浓度的分布越来越平坦。
高斯烟羽模型
在大气中,污染物的支配方程为 \[ \frac{\partial C_i}{\partial t} = - \nabla \cdot \vec{v} C_i + E_i + P_i - S_i \]
- \(C_i\) 为某个污染物的浓度
- \(E_i\) 为某个污染物的排放
- \(P_i\) 为某个污染物的化学作用
- \(S_i\) 为某个污染物的沉降作用
假设稳态、连续恒定点源、恒定风速,同时扩散采用 \( K \) 理论(不考虑风速,依旧是对流,就是高斯扩散,是高斯烟羽的一个特殊情况)。
- 稳态:\(\frac{\partial C_i}{\partial t}\) = 0
- 恒定风速:\( u \) 不随时空变化
- \( K \) 理论(类似热传导),扩散系数固定 \( K_x \), \( K_y \) , \( K_z \)
以 \( u \) 的方向为 \( x \) 方向
忽略化学和沉降,只考虑一个污染物,忽略 \( x \) 方向的扩散,可以得到 \[ u \frac{\partial C}{\partial x} = K_y \frac{\partial^2 C}{\partial y} + K_z \frac{\partial^2 C}{\partial z} + E_i \]
假设点源位于 \((0, 0, H)\) ,排放速率为 \( Q \)(单位:g/s)。
点源可表示为三维 Dirac δ 函数: \[ E_i(x, y, z) = \frac{Q}{u}\delta(x)\delta(y)\delta(z-H) = \frac{Q}{u}\delta(x)\delta(y)\delta(z-H) \]
最终的方程为 \[ u \frac{\partial C}{\partial x} = K_y \frac{\partial^2 C}{\partial y} + K_z \frac{\partial^2 C}{\partial z} + \frac{Q}{u}\delta(x)\delta(y)\delta(z-H) \]
该偏微分方程有解析解,采用格林函数法直接构造基本解。 \[ u \frac{\partial G}{\partial x} = K_y \frac{\partial^2 G}{\partial y} + K_z \frac{\partial^2 G}{\partial z} + \delta(x)\delta(y)\delta(z-H) \]
单位点源引起的浓度分布就是格林函数。
通过引入等效时间变量 \(\tau = \frac{x}{u}\), 可以得到标准的二维扩散方程(\(\tau\) 理解为时间)。
\[ \frac{\partial G}{\partial \tau} = K_y \frac{\partial^2 G}{\partial y} + K_z \frac{\partial^2 G}{\partial z} + \frac{1}{u}\delta(\tau)\delta(y)\delta(z-H) \]
\[ \frac{\partial G}{\partial \tau} - K_y \frac{\partial^2 G}{\partial y} - K_z \frac{\partial^2 G}{\partial z} = \frac{1}{u}\delta(\tau)\delta(y)\delta(z-H) \]
等式右边为排放强迫,\(\tau\) 理解为时间时,相当于在初始时刻瞬时释放了一定质量的污染物
初始条件为(在初始点为的浓度会无穷大,但是质量是守恒的): \[ G(\tau=0, y, z) = \frac{1}{u}\delta(\tau)\delta(y)\delta(z-H) \]
为了约束格林函数解,根据物理意义,在无穷远处,浓度应当为 0(边界条件).
可以直接写出格林函数解:
\[ G(x, y, z) = \frac{1}{4\pi \frac{x}{u} \sqrt{K_y K_z} } \exp( -\frac{u y^2}{4 K_y x} - \frac{u(z - H)^2}{4 K_z x}) \]
这就是瞬时点源在二维空间扩散方程下的解析解!
恢复尺度(乘上 \( Q \) ) \[ C(x, y, z) = \frac{Q}{4\pi \frac{x}{u} \sqrt{K_y K_z} } \exp( -\frac{u y^2}{4 K_y x} - \frac{u(z - H)^2}{4 K_z x} ) \]
由于地面 ( \( z= 0 \) )不可渗透(反弹),需满足边界条件: \[ \frac{\partial C}{\partial z}|_{z=0} = 0 \]
\[ C(x, y, z) = \frac{Q}{4\pi \frac{x}{u} \sqrt{K_y K_z} } \exp( -\frac{u y^2}{4 K_y x} - \frac{u(z - H)^2}{4 K_z x} ) \exp( -\frac{u y^2}{4 K_y x} - \frac{u(z + H)^2}{4 K_z x} ) \]
定义扩散尺度 \[ \sigma_y^2 = 2 K_y \frac{x}{u} \]
\[ \sigma_z^2 = 2 K_z \frac{x}{u} \]
最终可以得到高斯扩散模型解的一般形式。 \[ C(x, y, z) = \frac{Q}{2\pi u \sigma_y(x) \sigma_z(x)} \exp\left( -\frac{y^2}{2\sigma_y(x)^2} \right) \left[ \exp\left( -\frac{(z - H)^2}{2\sigma_z(x)^2} \right) + \exp\left( -\frac{(z + H)^2}{2\sigma_z(x)^2} \right) \right] \]
- \( C(x, y, z) \):污染物浓度(单位:g/m³)
- \( Q \):排放源的强度(g/s)
- \( u \):风速(m/s),假设为恒定
- \( \sigma_y(x), \sigma_z(x) \):在 \(x\) 方向上,横向(\(y\))和垂直(\(z\))的扩散系数,通常经验公式给出
- \( H \):污染源的有效排放高度(m)
- \(\exp\left( -\frac{y^2}{2\sigma_y^2} \right)\) 表示污染物在横向(\(y\))的高斯分布
- \(\exp\left( -\frac{(z - H)^2}{2\sigma_z^2} \right)\) 表示主烟团的垂直分布
- \(\exp\left( -\frac{(z + H)^2}{2\sigma_z^2} \right)\) 表示地面反射项(假设地面对污染物全反射)
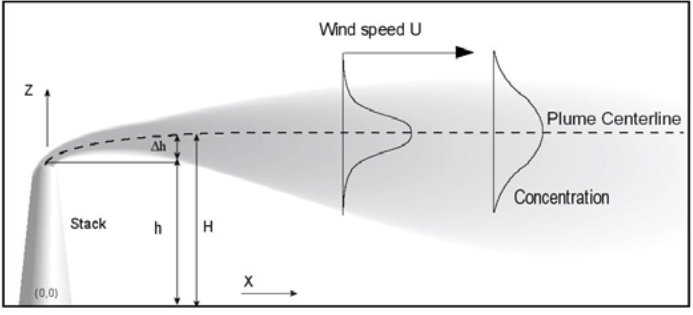
高斯烟团模型
烟团模型将连续的烟羽离散化,并计算离散时刻的烟团的浓度,然后允许烟团移动,其大小、强度等发生变化,直到下一个采样步骤,而受体处的总浓度是所有烟团贡献的总和。
\[ C(x, y, z, t) = \frac{Q}{(2\pi)^{3/2} \sigma_x \sigma_y \sigma_z} \exp\left( -\frac{(x-x_0(t))^2}{2\sigma_x^2} \right) \exp\left( -\frac{(y-y_0(t))^2}{2\sigma_y^2} \right) \exp\left( -\frac{(z-z_0(t))^2}{2\sigma_z^2} \right) \]
相当于一个高斯扩散随着风场飘动。
若每隔 1 秒释放一个 puff,则总体浓度每个puff的叠加。
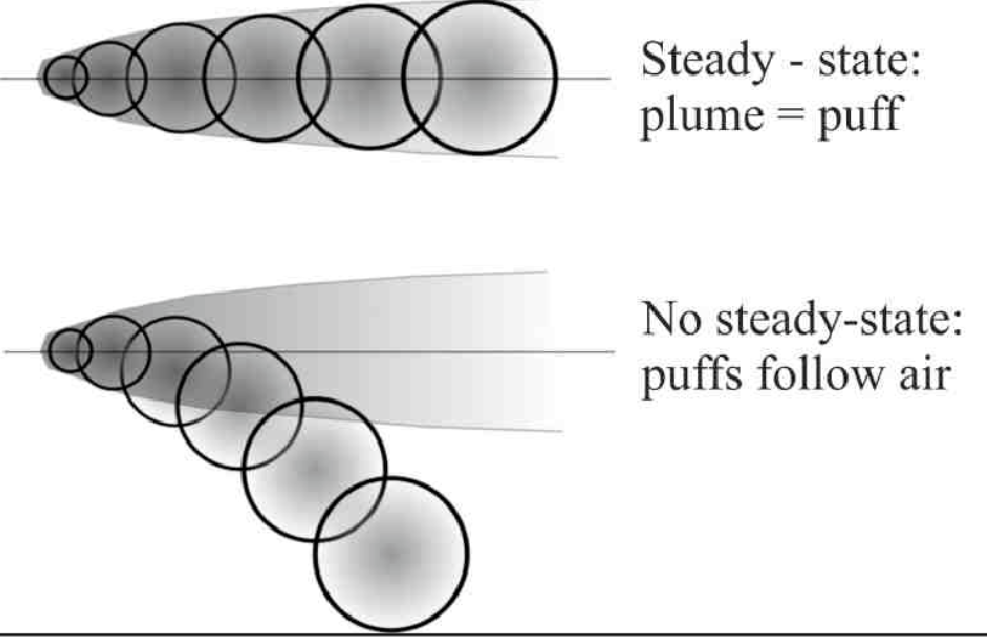
烟团法的一个传统缺点是需要释放大量烟团才能充分代表靠近源头的连续烟羽,如果烟团之间的距离最大超过 2σ,则可能会得到不准确的结果,同时烟团间隔减小到不超过 1σ,则可以获得更好的结果(烟团之间没有充分重叠)。
在风向变化时,一个已经释放的 Gaussian puff 的浓度分布并不会只是简单地“转弯”,如果风向持续改变,分布不再是各向同性的高斯,浓度分布会 拉长成“弯曲”路径,原本对称的高斯轮廓会变成 非轴对称形状,出现“剪切”或“拉扯”效应;因此需要 协方差矩阵 表示扩散形状。
\[ C_i(\mathbf{r}, t) = \frac{Q}{(2 \pi)^{3/2} \sqrt{\det \Sigma_i(t)}} \exp \left( -\frac{1}{2} (\mathbf{r} - \mathbf{r}_i(t))^T \Sigma_i^{-1}(t) (\mathbf{r} - \mathbf{r}_i(t)) \right) \] 其中
-
第 \( i \) 个羽流在时间 \( t \) 时的位置为:\(\mathbf{r}_i = (x_i, y_i, z_i)\)
-
烟团扩散的协方差矩阵(初始协方差矩阵)为: \[ \Sigma_i = \begin{bmatrix} \sigma_x^2 & 0 & 0 \\ 0 & \sigma_y^2 & 0 \\ 0 & 0 & \sigma_z^2 \end{bmatrix} \]
-
协方差矩阵随扩散增长,更新公式为: \[ \Sigma_i(t + \Delta t) = \Sigma_i(t) + D_{3D} \]
-
原始水平扩散矩阵: \[ D_{2D} = \begin{bmatrix} 2 K_x \Delta t & 0 \\ 0 & 2 K_y \Delta t \end{bmatrix} \]
-
旋转矩阵(旋转角度): \[ R = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \]
-
旋转后扩散矩阵: \[ D_{2D}^{rot} = R D_{2D} R^T \]
-
嵌入三维扩散矩阵中: \[ D_{3D} = \begin{bmatrix} D_{2D}^{rot} & 0 \\ 0 & 2 K_z \Delta t \end{bmatrix} \]
考虑烟团中心位置的变化,设当前风速为 \( u \),风向为 \( \theta \) (不考虑垂直运动)。 \[ \hat v = \begin{bmatrix} \cos \theta_{rad} \\ \sin \theta_{rad} \\ 0 \end{bmatrix} \]
\[ \mathbf{r}_i(t + \Delta t) = \mathbf{r}_i(t) + \Delta t \cdot u \hat v \]
在任意时间 \( t \),所有羽流的浓度叠加为:
\[ C(\mathbf{r}, t) = \sum_i C_i(\mathbf{r}, t) \]
电磁学
电力与引力相似,以距离的平方反比的方式衰减,这种关系叫做库仑力,但是这至对于静止的电荷有效,运动电荷之间还会产生磁力(洛伦兹力定律)。
[
\textbf{F} = q(\textbf{E} + \textbf{v} \times \textbf{B})
]
( \textbf{E} ) 和 ( \textbf{B} ) 分别为电场和磁场。
高斯定律(库仑力的等价形式,想象点电荷的球面):
[ \nabla \cdot \textbf{E} = \frac{\rho}{\varepsilon_0} ]
[ \nabla \cdot \textbf{B} = 0 ]
法拉第电磁感应定律
[ \nabla \times \textbf{E} = \frac{\partial \textbf{B}}{\partial t} ]
安培-麦克斯韦定律
[ c^2 \nabla \times \textbf{B} = \frac{\partial \textbf{E}}{\partial t} + \frac{J}{\varepsilon_0} ]
- ( \rho ):电荷密度,单位体积内的电荷量(单位:C/m³)。
- ( \varepsilon_0 ):真空介电常数,描述真空对电场的“响应能力”,数值约为
[ \varepsilon_0 \approx 8.854 \times 10^{-12} \ \mathrm{C^2 / (N \cdot m^2)} ] - ( \mathbf{B} ):磁感应强度(磁场),描述磁场对运动电荷的作用(单位:T,特斯拉)。
- ( \mathbf{J} ):电流密度,单位面积上的电流(单位:A/m²);
- ( c ):光速,在真空中 ( c = 3.00 \times 10^8 \ \mathrm{m/s} )。
电磁学
电力与引力相似,以距离的平方反比的方式衰减,这种关系叫做库仑力,但是这至对于静止的电荷有效,运动电荷之间还会产生磁力(洛伦兹力定律)。
[
\textbf{F} = q(\textbf{E} + \textbf{v} \times \textbf{B})
]
( \textbf{E} ) 和 ( \textbf{B} ) 分别为电场和磁场。
高斯定律(库仑力的等价形式,想象点电荷的球面):
[ \nabla \cdot \textbf{E} = \frac{\rho}{\varepsilon_0} ]
[ \nabla \cdot \textbf{B} = 0 ]
法拉第电磁感应定律
[ \nabla \times \textbf{E} = \frac{\partial \textbf{B}}{\partial t} ]
安培-麦克斯韦定律
[ c^2 \nabla \times \textbf{B} = \frac{\partial \textbf{E}}{\partial t} + \frac{J}{\varepsilon_0} ]
- ( \rho ):电荷密度,单位体积内的电荷量(单位:C/m³)。
- ( \varepsilon_0 ):真空介电常数,描述真空对电场的“响应能力”,数值约为
[ \varepsilon_0 \approx 8.854 \times 10^{-12} \ \mathrm{C^2 / (N \cdot m^2)} ] - ( \mathbf{B} ):磁感应强度(磁场),描述磁场对运动电荷的作用(单位:T,特斯拉)。
- ( \mathbf{J} ):电流密度,单位面积上的电流(单位:A/m²);
- ( c ):光速,在真空中 ( c = 3.00 \times 10^8 \ \mathrm{m/s} )。
编程技能
文档工具
mdbook 的备忘录
1. 命令
- 开始:
mdbook init [path/to/book] [--title "some"] [--ignore] - 渲染:
mdbook build [-o],默认当前工作目录就是根目录 - 调试:
mdbook watch [-o],默认当前工作目录就是根目录 - 调试:
mdbook clean,默认当前工作目录就是根目录 - 服务:
mdbook serve path/to/book -p 8000 -n 127.0.0.1
2. 结构
SUMMARY.md用来表明层次结构,并导入章节对应的 Markdown 文件。
其格式非常严格,具体结构如下:
# Summary <!-- 标题, 可选 -->
--- <!-- 生成 HTML 渲染行 -->
[前言](./prefix.md) <!-- 前缀章节, 可选 -->
<!-- 可以没有标题[]() -->
- [文档工具]() <!-- 草稿章节, HTML 中的禁用链接 -->
- [mdbook 的备忘录](./docs/chapter_1.md) <!-- 编号章节, 可以嵌套 -->
[后记](./Suffix.md) <!-- 后缀章节, 可选 -->
注意 章节对应的 Markdown 文件不存在 mdbook 会自动创建空文件
3. 配置
book.toml 为整本书的配置文件
[book]
authors = ["xiaolh"]
language = "cn"
multilingual = false # 是否支持多语言
src = "src"
title = "xiao's notes"
description = "mdbook" # 作为元信息添加到 html<head>中
# 默认预处理
[preprocessor.index] # 将所有名为 README.md 的章节文件转换为 index.md
[preprocessor.links] # 嵌入一些代码,rust有用
# 第三方预处理器
[preprocessor.mathjax]
# 自定义预处理器
[preprocessor.random]
command = "python random.py"
# 渲染配置
[output.html]
mathjax-support = true # 公式支持
additional-css = ["custom.css"] # 自定义样式,一般用不着
[output.html.search]
limit-results = 15
其中多语言支持后的结构
book/
├── en/ # 英文
│ ├── SUMMARY.md
│ ├── chapter_1.md
│ ├── chapter_2.md
│ └── ...
├── zh/ # 中文
│ ├── SUMMARY.md
│ ├── chapter_1.md
│ ├── chapter_2.md
│ └── ...
├── book.toml
└── ...
4. 公式
内联方程由 \\( 和 \\) 分隔,
块方程由 \\[ 和 \\] 分隔。
\[ \frac{\partial c}{\partial t} = - \nabla \cdot \mathbf{v} c \]
5. 持续部署
GitHub Pages 对 mdbook 提高了非常好的支持。
点击 Settings => 点击 Pages => 在 source 中选择 GitHub Actions => 点击 mdbook 中的 Configure。
会自动生成一个 GitHub Actions 的配置文件 .github/workflows/mdbook.yml,
不用修改,点击保存既可以,稍微等一会,就可以打开 GitHub Pages 提供的网站。
6. 经常忘记的 Markdown 语法
链接 和 图片
[mdBook](mdBook.md).
[mdBook](https://github.com/rust-lang/mdBook).

开发工具
WSL
安装
wsl --install
文件共享
从 Windows 访问 WSL 文件
在文件资源管理器地址栏输入
\\wsl$\Ubuntu\home\
从 WSL 访问 Windows 文件
Windows 的盘符会自动挂载在 /mnt/ 下
xiaolh@DESKTOP-B3VFKS8:~/work$ ls /mnt/
c d wsl wslg
xiaolh@DESKTOP-B3VFKS8:~/work$
程序、脚本联动
在 WSL 中运行 Windows 程序
explorer.exe . # 打开当前文件夹在 Windows 文件管理器中
code . # 如果已安装 VSCode,会打开当前目录
xiaolh@DESKTOP-B3VFKS8:~$ which code
/mnt/d/apps/VSCode/bin/code
docker
安装
在 window 中安装 docker 推荐方案使用 Docker Desktop。
Docker Desktop 实际上在后台启动一个 Linux 虚拟机(WSL2 后端), 你可以在其中运行 Docker 容器,而不需要再手动管理 daemon(Docker的服务)。
下载安装包, 然后在安装的时候选择 WSL 2 backend
docker中的核心概念
- 镜像: 就像可执行程序(运行某个程序所需的所有内容,包括系统库)
- 容器:就行进程,是一个运行的镜像,Image+运行时状态
- 网络:Docker 默认会为容器分配虚拟网络,使其相互隔离
- 数据卷: Docker 提供的持久化存储机制,可以把数据挂载在容器外部
- Dockerfile: 定义镜像构建过程的脚本(可以从一个基础镜像开始)
- Docker 引擎:一个运行时,容器的调度器,整个容器运行的“操作系统”
常用命令
镜像相关
| 命令 | 说明 |
|---|---|
docker images | 列出本地镜像 |
docker pull <镜像名> | 从 Docker Hub 拉取镜像 |
docker build -t <自定义镜像名> . | 根据 Dockerfile 构建镜像 |
docker rmi <镜像ID或名称> | 删除镜像(不能有依赖容器) |
docker tag <镜像ID> <新名称> | 重命名镜像 |
容器相关
| 命令 | 说明 |
|---|---|
docker ps | 查看正在运行的容器 |
docker ps -a | 查看所有容器(包括已停止) |
docker run <镜像名> | 运行一个容器 |
docker run -it <镜像名> /bin/bash | 交互式运行并进入容器 |
docker exec -it <容器名或ID> /bin/bash | 进入已经运行的容器 |
docker stop <容器ID或名称> | 停止容器 |
docker start <容器ID或名称> | 启动已停止的容器 |
docker restart <容器ID或名称> | 重启容器 |
docker rm <容器ID或名称> | 删除容器(需先停止) |
docker logs <容器ID或名称> | 查看容器输出日志 |
网络与数据卷
| 命令 | 说明 |
|---|---|
docker network ls | 列出网络 |
docker network create <名称> | 创建网络 |
docker volume ls | 列出数据卷 |
docker volume create <名称> | 创建数据卷 |
docker run -v <本地路径>:<容器路径> | 挂载本地目录到容器 |
清理命令
| 命令 | 说明 |
|---|---|
docker system prune | 清理无用数据(停止容器、悬挂镜像等) |
docker container prune | 清理所有停止的容器 |
docker image prune | 清理未使用的镜像 |
docker volume prune | 清理未使用的卷 |
其他实用命令
| 命令 | 说明 |
|---|---|
docker inspect <容器或镜像> | 查看详细信息(JSON) |
docker cp <容器>:<路径> <本地路径> | 从容器拷贝文件到本地 |
docker stats | 查看容器资源占用情况 |
Jupyter Notebook
简介
Jupyter Notebook 是一个基于 Web 的交互式计算环境,可以用来创建和共享包含代码、方程、可视化和文本的文档。支持多种编程语言(如 Python、R、Julia 等)。
运行
jupyter notebook --ip=0.0.0.0 --port=8888 --no-browser
查看访问地址(默认需要token)
jupyter server list
用浏览器打开地址即可
常用快捷键
-
运行当前单元格并选中下一个:
Shift + Enter -
运行当前单元格但保持选中状态:
Ctrl + Enter -
中断代码运行:
i i(连按两次 i) -
插入新单元格(在上方):
a或者A -
插入新单元格(在下方):
b -
删除当前单元格:
D D(连按两次 d) -
Code(代码单元格)
-
Markdown(文本单元格)
rust
主要思想
一门把编程习惯 用语法表达出来的编程语言。
什么变量?
是一段内存的标识,也就是这段内存的别名;
定义变量就是申请内存(申请内存也可以通过系统调用来完成)。
内存存储了所有数据(包括执行的代码,代码区不讨论),大致可以分为三个区域(简化的说): a. 全局/静态存储区: static float values[1000]; b. 栈: 函数中的普通局部数据 c. 堆: 动态分配的数据
定义变量,可以理解为在栈结构上,保存了(开辟了一片内存)一段已知大小的数据 或者 描述一段堆内存的信息(指针)。 堆上可以定义变量吗? 堆上只可以存储数据,这段数据的描述存在栈上,这个描述有个名字,叫变量(一般都是指针类型,智能指针)。
怎么去描述一段连续内存? 内存地址 + 长度; 这种结构的大小是已知的(指针的大小已知)。
栈的结构是动态的,随着函数的调用和返回动态增大或者减小。
随着函数的返回,该函数的栈桢消失(只是改变了栈顶寄存器),返回之后,函数内部定义的变量也就没办法引用,该函数栈桢中的数据理论上应该是无效的。
语义非常清晰,但是在C语言(类似)的编程中,会出现一些编程错误(应该程序员彻底理解语义之后,自己避免): 1) 函数有可能返回了指向该函数栈桢中数据的指针? 悬垂指针 2) 函数申请的堆上的数据结构(该函数栈桢中数据保存的是描述一段连续内存的内存)是否释放了? 什么时候应该释放(不释放,内存会爆炸、内存泄漏)? 3) 函数有没有权限去修改外部调用函数栈桢中的数据: 多线程中的数据竞争问题;
不同语言对变量(内存)的访问、 修改、 销毁处理思路很不一样。
// 对于堆上的数据,谁去销毁
a. C/C++: malloc/free(程序员自己去做);
b. python/java/js:垃圾回收机制(运行时);
c. rust: 基于所有权模型、生命周期的自动堆内存释放(编译阶段);
所有权明确了谁去销毁;
生命周期明确了销毁前,不会有其他引用,避免悬垂指针。
单一可变引用,明确了数据不出现竞争情况。
// 避免悬垂指针; rust: 生命周期: 结构体中的生命周期,确实很烦人,但是也是有必要的; 大部分语言不考虑这个问题,程序员自己解决;
强大的抽象能力
rust: 模板展开(泛型编程 + trait绑定;)
并发编程
rust: 异步解决方案: Future async/awaite;
函数式编程
&String: 包含容量信息(可变的数据结构); &str: 不包含容量信息; 切片的一种;
##: 在良好实现的分层机制中,对于某一层的实现者而言,下一层的绝大部分是不需关心的。 随着我们创造越来越多、越来越高层的抽象,编程实现会变得更加简单,但成为专业程序员也越来越难。
事实上,如果要从整个技术界中选一个本科教育一般不大重视、但又极度有价值的术语,我会选闭包和高阶函数?
返回函数,那么函数确实是一个动态数据接口,应该存储在堆上?
闭包本身是一个数据结构
struct Closure { captured_variables: ..., // 存储捕获的环境变量 // 逻辑代码的调用是编译器插入的,Closure 实现了 Fn、FnMut 或 FnOnce }
fn(Args) -> Output
机器学习
机器学习是一种寻找数据中蕴含的关系( \(y = f(x)\) )的方法。与物理思维不同,机器学习是依靠数据去拟合参数,从而抽取数据中蕴含的可能关系。
物理思维是通过基本定律(因果)的约束,去推导关系。比如已知加速度和速度的定义 \[ a = \frac{dv}{dt} \] \[ v = \frac{ds}{dt}\] 可以得到位移的公式(位移与时间的关系) \[ s = \frac{1}{2}at^2 + v_0 t + s_0 \]
数据驱动的含义是指,不去在意因果,只关注关系。
因果是人类思维执着的东西,虽然机器学习在一些领域能够拟合出较好关系,我们仍然会执着于解释,为什么机器学习有这样的能力。大量的神经节点的堆叠真的能表现出一定的智慧(什么是智慧?表现出的智慧具体是指什么?),还是只是某种更为高效的信息存储手段(记忆)和更为强大的信息检索能力(所谓的文本生成)。
关系的准确描述需要数学语言,不管你是否想给这个关系赋予其物理意义。经典的统计回归算法会给定一个函数形式,如何给定?先感性地观察样本(肉眼看),可以大致看出变量之间满足什么关系,比如线性型、指数型、对数型、多项式型、周期型。然后给出一个可能的函数形式(可以是复合函数),该函数会有一些待定的参数,最简单函数形式就是多元线性回归
\[ y = a_1 x_1 + a_2 x_2 + ... + a_n x_n + b\]
再通过一组的样本,去确定参数 \(a\) 和 \(b\)。这样基本上能够抓住主要矛盾(毕竟肉眼就可以看出来),但是很难提升模型的精度(给定未知样本,得到的 y 与实际观测的相差可能很大)。
很多物理定律的获得其实也采用了这种方法,不过其待确定的参数通常很少,同时物理的视角更聚焦公式的意义,也就是为什么公式会是这样的(机器学习关注的是新样本来了准不准,只要准就行,并不关注公式及其参数的意义,只要在不准的时候,才会去审视为什么)。比如万有引力定律描述两个质量体之间因引力而相互吸引的关系,这个定律并非从更基本的定律严格推导而来,而是通过观察、实验(如开普勒行星运动定律)和逻辑推理总结出来的经验定律,也存在一个待定参数(万有引力常数 \(G\) ,卡文迪许扭秤实验获得大量样本,也会用最小二乘法去确定参数值)。万有引力定律能够预测很多天文现象,但是我们并不满足于此,而是更执着于为什么会是这样(广义相对论)。
同时,不是每次都能轻易的看出来关系的大致函数形式(系统物理机制不完全清楚或过于复杂、数据庞杂,但难以建立明确数学方程、存在高度非线性或高维特征空间),另一类机器学习算法,并不预设 \(f\) 的形式,而是借助如神经网络、支持向量机、随机森林等算法,去可以去拟合任意未知函数形式(也是目前机器学习这么火的原因),类似傅里叶级数,通过基本函数的组合(三角函数),从而可以拟合任意函数(函数的性质有限制,但是应该不多)。
对于数据集中蕴含的复杂关系的情况,我们可以使用这种方案。比如对于语言、文字、图片,我们每个人去看,去听,去观察之后,都能得到差不多的结论(至少在语义或者形式上不会有太大歧义),说明语言识别,图片识别一定存在某种关系,但是这种关系从直觉上很难给出一个函数形式,那么就可以用神经网络去做拟合。
为了能更好地解决更复杂的问题,出现了越来越复杂的拓扑结构,同时,也使得参数的拟合变得越来越困难,并且消耗巨量资源,人力和资源的投入是否会越来越没有性价比,我也十分好奇这是否是一条有深度的、可持续发展的路。因此决定研究一下相关技术,希望自己不会迷失在这铺天盖地的宣传中。
在我理解,作为高级智慧生物,我们真正智慧的地方是抽象的能力,从有限的经验中,总结出更一般的模型(归纳),这个抽象不是一般意义上的堆积性的归纳,而是会创造脱离经验的,蕴含意义更加广泛的符号,用这些符号来描述关系,期待得到更具普适性的认知模型,虽然也存在黑天鹅的问题,模型并不一定就是宇宙的真理,就像牛顿力学被相对论替换一样,我们抽象出了的模型,只能解释我们目前收集到的所有经验,并可能能预测一些未知的经验,但是这种抽象之后的模型,是人类目前最能拿得出手的东西。模型成体系的出现,并在之后的实践过程中,被大量未知的经验反复的认证过,就会形成一个完整的理论,一门学科,比如物理、化学、生物。
那么机器的智慧,到底是什么样的呢?
神经网络
Deep learning is a general framework for function approximation.
神经网络是由神经元堆叠而成,单个神经元的公式如下
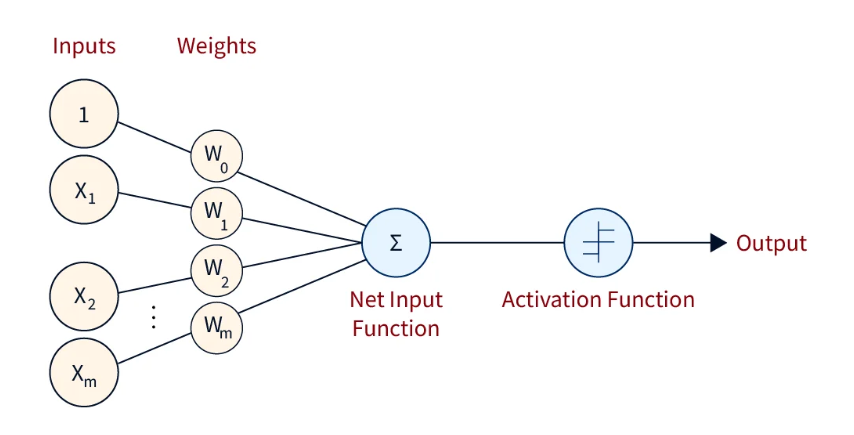
\[ y = \sigma(wx + b) = \sigma(\sum_{i=1}^N (w_i x_i) + b) \]
- \( x \) 是输入向量,也被叫做输入层,第0层
- \( \sigma \) 是激活函数(如 sigmoid, ReLU 等)
- \( N \) 是输入向量的维度
- \( w, b\) 是待确定的参数, \(w\) 是权重向量,\(b\) 是偏执
单层神经网络是由神经元堆叠而成,包含一个隐藏层( \(l=1\) ),和一个输出层( \(l=2\) )
\[ y^2 = w^2y^1 + b^2 \]
其中 \(y^1\) 为隐藏层的输出 \[ y_j^1 = \sigma(w_j^1x + b^1) \]
- 上标标识第几层
Neural nets are powerful approximators: any continuous function can be arbitrarily well approximated on a compact using a three-layer fully connected network F = f1 ◦ σ ◦ f2 (universal approximation theorem, Cybenko, 1989, Hornik, 1991).
根据通用逼近定理(Universal Approximation Theorem), 如果激活函数是非线性且满足某些条件(如连续、有界、非恒等于零), 那么一个具有足够多的神经网络节点,可以在紧集上逼近任意连续函数 \(f: \mathbb{R}^n \to \mathbb{R}\)
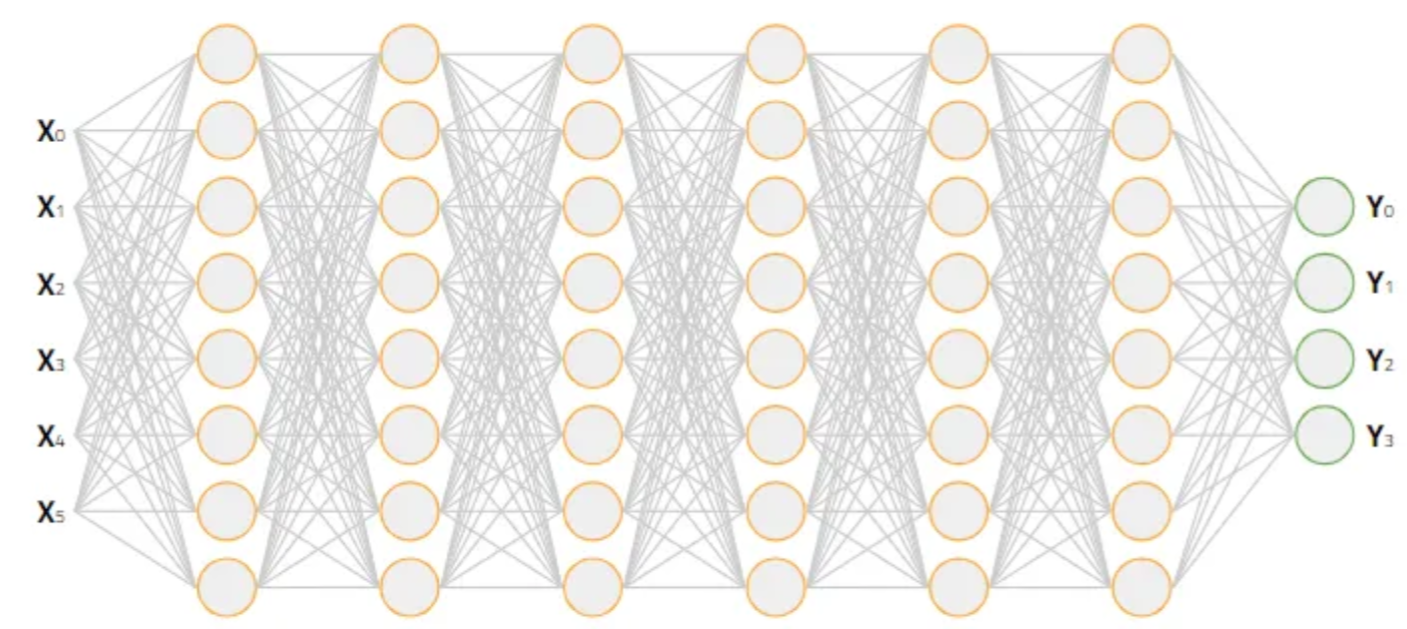
单层神经网络可以去拟合任意函数形式,但是前提条件是具有足够多的神经网络节点,可能是无限多,同时未知函数形势是需要连续的(不管这个条件)。但毕竟我们不能构建无限多的神经网络节点, 我们只能从其他方面入手,在有限的资源下(节点个数),获得更好的效果。 其中一个方式就是多层神经网络(这也是深度学习中深度的含义)。
从单层神经网络的公式中可以看出(在最外层添加一个激活函数),神经网络的定义是一种递归结构,很容易把单层神经网络推广到多层。 \[ y^l = \sigma(w^ly^{l-1} + b^l) \]
\[ y^0 = x \]
- \(1 \in \{1, 2, ..., n\} \),为层的标识,第几层。
- \(w^l \) 是权重矩阵。
我们希望在不改变神经元个数的情况,通过增加神经网络的层数,来获得更好的拟合能力。
为了什么能这样?我们期待的是一种特征的分层提取。
训练
训练神经网络,本质上就是要使得所有样本的误差最小(也就是所有样本的输出都很满意,符合实际的情况)。 我们要定义误差函数,注意这是一个关于权重的函数。
\[ C = f(W, B) = \sum_{i=1}^N (\Arrowvert y_i^L - y_i^{obs} \Arrowvert) \]
对于单个样本(误差函数也可以有其他形式)。 \[ C = f(W, B) = (\Arrowvert y^L - y^{obs} \Arrowvert) = \sum_{j=1}^J (y_j^L - y_j^{obs})^2 \]
要求 \(W, B\) 使得 \(C\) 最小,这是一个高维函数的极值问题,理论上找不到全局最小值,我们只能用梯度下降法去找到一些距地最小值。首选随机给定初始权重\(W^0, B^0\)。 然后计算 \(\nabla C\)
\[ \nabla C_w = \{\frac{\partial C}{\partial W} \}\] \[ \nabla C_b = \{\frac{\partial C}{\partial B} \}\]
如何求解梯度?
设每个激活函数的输入为 \[ z^l = w^ly^{l-1} + b^l \]
根据链式求导法则,可以得到
\[ \delta^L = \nabla C_y^L \otimes \sigma'(z^L) \]
\[ \delta^l = (w^l)^T \nabla \delta^{l+1} \otimes \sigma'(z^l) \]
\[ \nabla C_b^l = \delta^l \]
\[ \nabla C_w^l = \delta^l {y^{l-1}}^T \]
- \(\sigma'\) 为激活函数的导数
最后根据梯度更新权重(注意要根据所有样本的来更新权重)。
\[ W^{t+1} = W^{t} - \eta \frac{1}{n}\sum \nabla C_w \] \[ B^{t+1} = B^{t} - \eta \frac{1}{n}\sum \nabla C_b \]
这就是反向传播算法。
激活函数
下面是一些常见激活函数及其导数,这些在反向传播算法中非常关键。
Sigmoid 函数(Logistic) 由 sigmoid 神经元构成的网络可以逼近任意函数,sigmoid也是神经网络激活函数的入门款。 \[ \sigma(x) = \frac{1}{1 + e^{-x}} \]
\[ \sigma'(x) = \sigma(x)(1 - \sigma(x)) \] Sigmoid 函数 在 x 比较大或者比较小时,其斜率会非常小, 此时如果误差函数选用的是均方误差(平均绝对误差), 那么会导致梯度下降法的步长变得很小,从而影响拟合的效率。
Tanh 函数(双曲正切) 与 sigmoid 函数不同,tanh 的输出范围是 (−1,1)。这种对称性使得在训练中,梯度传播的效果往往更好,尤其是在深层网络中可以减少梯度偏移问题,从而加速收敛。 \[ \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \]
\[ \tanh'(x) = 1 - \tanh^2(x) \] 存在一些理论推理以及实验数据表明,在很多情况下,tanh 神经元的表现优于 sigmoid。
ReLU(Rectified Linear Unit)
ReLU 的优点在于它一部分神经元输出为 0,有效地进行选择性激活,相比 sigmoid 和 tanh 无需指数计算,同时梯度不会饱和。极大缓解了**梯度消失(vanishing gradient)**问题,对于多层神经网络的训练很有帮助。 \[ \mathrm{ReLU}(x) = \max(0, x) \]
\[ \mathrm{ReLU}'(x) = \begin{cases} 1, & x > 0 \ 0, & x \le 0 \end{cases} \]
Softplus(ReLU 的平滑版本) ReLU存在负半轴的“死亡”问题(dead neuron),一旦某个神经元的输入一直小于 0,它就永远输出 0,永远不更新梯度,彻底失活。用一个平滑过渡,能够一定程度缓解这些问题。
\[ \mathrm{Softplus}(x) = \ln(1 + e^x) \]
\[ \mathrm{Softplus}'(x) = \frac{1}{1 + e^{-x}} = \sigma(x) \]
误差函数(代价函数、损失函数)
均方误差
\[ \mathcal{L}_{\mathrm{MSE}} = \frac{1}{n} \sum (y_i - \hat{y}_i)^2 \]
梯度 \[ \frac{\partial \mathcal{L}}{\partial \hat{y}_i} = 2(\hat{y}_i - y_i) \]
平均绝对误差
\[ \mathcal{L}_{\mathrm{MAE}} = \frac{1}{n} \sum |y_i - \hat{y}_i| \]
梯度 \[ \frac{\partial \mathcal{L}}{\partial \hat{y}_i} = \begin{cases} -1, & \hat{y}_i > y_i \ 1, & \hat{y}_i < y_i \ \text{undefined}, & \hat{y}_i = y_i \end{cases} \]
交叉熵 交叉熵损失函数 感觉是从 负对数似然函数而来。
负对数似然函数的定义
假设我们有一个分类问题,给定输入 \( x \),模型的预测标签 \( y \) 的概率分布为 \( p(y|x, \theta) \),其中 \( \theta \) 是模型的参数。负对数似然函数定义为:
\[ \text{NLL} = - \log p(y | x, \theta) \]
最大似然估计与交叉熵
假设我们有一个训练数据集 \( D = {(x_i, y_i)}_{i=1}^N \),每个样本 \( x_i \) 的标签 \( y_i \) 从真实分布中独立抽取。
为了使模型的参数 \( \theta \) 最优,我们使用最大似然估计(MLE),即通过最大化训练数据集上所有样本的似然函数来找到最优的模型参数。
对于整个数据集的似然函数 \( L(\theta) \),可以表示为:
\[ L(\theta) = \prod_{i=1}^N p(y_i | x_i, \theta) \]
对应的对数似然函数为:
\[ \log L(\theta) = \sum_{i=1}^N \log p(y_i | x_i, \theta) \]
负对数似然函数为:
\[ \text{NLL} = - \log L(\theta) = - \sum_{i=1}^N \log p(y_i | x_i, \theta) \]
与交叉熵的关系
在交叉熵的定义中,考虑每个样本 \( i \) 的标签 \( y_i \) 和模型预测概率分布 \( p(\hat{y}|x_i, \theta) \)。交叉熵损失函数为:
\[ H(p, \hat{p}) = - \sum_{y} p(y) \log \hat{p}(y) \]
在分类任务中,真实标签 \( y_i \) 通常是从一个真实分布 \( p(y) \) 中抽取的,因此我们可以把交叉熵看作是每个样本的负对数似然。对于每个样本,交叉熵损失为:
\[ H(p, \hat{p}) = - \log p(y_i | x_i, \theta) \]
推导过程
将负对数似然函数和交叉熵联系起来:
-
对于每个样本 \( i \),负对数似然为 \( - \log p(y_i | x_i, \theta) \),这正是交叉熵的定义。
-
对整个数据集 \( D \),交叉熵损失(对所有样本的损失平均值)为:
\[ H(p, \hat{p}) = - \frac{1}{N} \sum_{i=1}^N \log p(y_i | x_i, \theta) \]
这与负对数似然函数的形式完全相同,区别在于交叉熵是对所有样本的平均值。
- 负对数似然函数可以看作是交叉熵的一个特例,特别是在分类问题中。
- 在最大似然估计中,我们通过最大化数据集上样本的似然函数来训练模型,而交叉熵可以被看作是负对数似然的平均值。
最终我们可以得出结论:交叉熵是负对数似然函数的平均值,并且它们在多分类或二分类问题中是等价的。
对于单个样本,交叉熵损失函数的定义为
\[ \mathcal{L}_{\mathrm{CE}} = - \sum y_i^{obs} \ln(y_i) \]
对于神经网络的输出层,如果套了一层 Softmax,这时用交叉熵损失函数作为误差函数,会使得偏导计算十分方便。
对于Z的求导 \[ \frac{ \partial \mathcal{L}}{ \partial Z_i^L} = y_i^L - y_i^{obs} \]
其中 \[ Z_i^L = \sigma(z_i^L) \]
交叉熵与Softmax函数结合在一起,也叫 Softmax 损失。
那交叉熵的直观含义是什么呢?我们应该如何理解它?在信息论中对交叉熵有一个标准的解释方式。
粗略地说,交叉熵衡量的是“惊讶”程度。具体而言,我们的神经元试图计算的是函数 \( f \),但实际上它计算的是 \( \hat{f} \) 假设我们将 \( \hat{f} \) 视为 \( f \)的概率估计值,那么交叉熵就衡量了当我们得知 \( \hat{f} \) 的真实值时,我们“平均上感到多惊讶”。如果输出结果与我们预期一致,我们的“惊讶”就小;如果结果出乎意料,“惊讶”就大。
训练优化策略
几乎所有的机器学习优化算法都是基于梯度下降的算法。
依据计算目标函数梯度使用的数据量的不同,有一种梯度下降的变体,即随机梯度下降(stotastic gradient descent, SGD),每次只用随机的部分的样本用于更新权重。这样可以加快算法的收敛速度(比较不用每次都把全部的样本跑一次)。
另一类优化,是考虑每次走多远。
比如用 Hessian 优化,考虑二阶项,加速误差函数的收敛速度。 \[\Delta w = -H^{-1} \nabla C \] 但是求 Hessian 矩阵比较消耗资源。
直观地说,Hessian优化的优势在于它不仅引入了关于梯度的信息,还引入了关于梯度变化的信息。基于动量的梯度下降法基于类似的直觉,但避免了使用大量的二阶导数矩阵。
基于动量的梯度下降法的数学定义需要引入一个速度量,速度量和权重一一对应。 \[ v' = \mu v - \eta \nabla C \] \[ w' = w + v' \]
对于速度的更新,可以想象单位质量为 1 的小球,在力 \( \eta \nabla C \) 的作用下,在单位时间 动量的变化。对 \( w \) 的更新,可以想象程单位时间在速度 \( v' \) 的作用下发生的位移。如果我们直线下坡会发生什么情况,每一步沿着斜坡向下,速度都会增加,因此我们会越来越快地接近谷底。这种特性使得动量方法相比标准梯度下降法能够更快地收敛。\( \mu \) 相当于摩擦系数,可以在加速学习的同时避免“冲过头”的风险。
在现有的梯度下降实现中,几乎无需改动就可以引入动量机制。通过这种方式,我们可以在不引入Hessian巨大计算代价的前提下,部分利用梯度变化的信息,从而获得类似Hessian方法的优势。
最后是如何避免陷入某些不好的距地最小值,而去寻找更好的最小值位置,比如用自适应步长技术来避免局部最小值(Adagrad,RMSProp,Adam),比如 RMSProp 使用二阶矩估计来调整各个参数的学习率,每个参数按其历史梯度动态调整步长,避免大步震荡或小步卡顿。
正则化
拥有大量自由参数的模型可以描述极其广泛的现象。即使这样的模型与现有数据吻合得很好,也并不意味着它是一个好的模型。这可能仅仅意味着模型拥有足够的自由度,几乎可以描述任何给定规模的数据集,而无法捕捉到任何对潜在现象的真正洞察。当这种情况发生时,模型虽然适用于现有数据,但无法推广到新的情况。对一个模型的真正考验是它能否在从未接触过的情况下做出预测
检测过拟合最明显的方法是使用上述方法,在网络训练过程中持续追踪测试数据的准确率。如果我们发现测试数据的准确率不再提升,就应该停止训练。
增加训练样本,也可以防止过度拟合,样本的size应当比权重要多吧!
除了以上方法,也可以采用正则化技术,最常用的正则化技术,有时也称为权重衰减或 L2 正则化。L2 正则化的思想是在成本函数中添加一个额外的项,称为正则化项。
\[ \frac{\lambda}{2n} \sum w^2 \]
直观地说,正则化的作用是使网络 在其他条件相同的情况下,更喜欢学习较小的权重。换句话说,正则化可以被视为在寻找小权重和最小化原始成本函数。
\[ \nabla C_w^l = \delta^l {y^{l-1}}^T + \frac{\lambda}{n}w \]
\[ W^{t+1} = (1-\frac{\eta \lambda}{n})W^{t} - \frac{1}{n}\sum \nabla C_w \]
对于 SGD (每次m个样本):
\[ W^{t+1} = (1-\frac{\eta \lambda}{n})W^{t} - \frac{1}{m}\sum \nabla C_w \]
权重越小,从某种意义上来说复杂度就越低,因此能够更简单、更有力地解释数据,因此应该优先考虑。有一种观点认为,在科学上我们应该遵循 更简单的解释,除非被迫不这样做。权重较小意味着,即使我们随意更改一些随机输入,网络的行为也不会发生太大变化。
dropout 是一种类似集合平均的正则化技术,但是是网络内部的集合平均。
人为地扩大训练数据(样本需要具备,平移,旋转等对称性)。
权重初始化
减低权重的标准差,避免激活函数的输入,由于卷积的影响,变成很偏坦的高斯分布,从而导致隐藏层达到饱和,难以训练。
案例代码
"""
An improved version of network.py, implementing the stochastic
gradient descent learning algorithm for a feedforward neural network.
Improvements include the addition of the cross-entropy cost function,
regularization, and better initialization of network weights. Note
that I have focused on making the code simple, easily readable, and
easily modifiable. It is not optimized, and omits many desirable
features.
"""
#### Libraries
# Standard library
import json
import random
import sys
# Third-party libraries
import numpy as np
#### Define the quadratic and cross-entropy cost functions
class QuadraticCost(object):
@staticmethod
def fn(a, y):
"""Return the cost associated with an output ``a`` and desired output
``y``.
"""
return 0.5*np.linalg.norm(a-y)**2
@staticmethod
def delta(z, a, y):
"""Return the error delta from the output layer."""
return (a-y) * sigmoid_prime(z)
class CrossEntropyCost(object):
@staticmethod
def fn(a, y):
"""Return the cost associated with an output ``a`` and desired output
``y``. Note that np.nan_to_num is used to ensure numerical
stability. In particular, if both ``a`` and ``y`` have a 1.0
in the same slot, then the expression (1-y)*np.log(1-a)
returns nan. The np.nan_to_num ensures that that is converted
to the correct value (0.0).
"""
return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))
@staticmethod
def delta(z, a, y):
"""Return the error delta from the output layer. Note that the
parameter ``z`` is not used by the method. It is included in
the method's parameters in order to make the interface
consistent with the delta method for other cost classes.
"""
return (a-y)
#### Main Network class
class Network(object):
def __init__(self, sizes, cost=CrossEntropyCost):
"""The list ``sizes`` contains the number of neurons in the respective
layers of the network. For example, if the list was [2, 3, 1]
then it would be a three-layer network, with the first layer
containing 2 neurons, the second layer 3 neurons, and the
third layer 1 neuron. The biases and weights for the network
are initialized randomly, using
``self.default_weight_initializer`` (see docstring for that
method).
"""
self.num_layers = len(sizes)
self.sizes = sizes
self.default_weight_initializer()
self.cost=cost
def default_weight_initializer(self):
"""Initialize each weight using a Gaussian distribution with mean 0
and standard deviation 1 over the square root of the number of
weights connecting to the same neuron. Initialize the biases
using a Gaussian distribution with mean 0 and standard
deviation 1.
Note that the first layer is assumed to be an input layer, and
by convention we won't set any biases for those neurons, since
biases are only ever used in computing the outputs from later
layers.
"""
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)/np.sqrt(x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]
def large_weight_initializer(self):
"""Initialize the weights using a Gaussian distribution with mean 0
and standard deviation 1. Initialize the biases using a
Gaussian distribution with mean 0 and standard deviation 1.
Note that the first layer is assumed to be an input layer, and
by convention we won't set any biases for those neurons, since
biases are only ever used in computing the outputs from later
layers.
This weight and bias initializer uses the same approach as in
Chapter 1, and is included for purposes of comparison. It
will usually be better to use the default weight initializer
instead.
"""
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]
def feedforward(self, a):
"""Return the output of the network if ``a`` is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
lmbda = 0.0,
evaluation_data=None,
monitor_evaluation_cost=False,
monitor_evaluation_accuracy=False,
monitor_training_cost=False,
monitor_training_accuracy=False):
"""Train the neural network using mini-batch stochastic gradient
descent. The ``training_data`` is a list of tuples ``(x, y)``
representing the training inputs and the desired outputs. The
other non-optional parameters are self-explanatory, as is the
regularization parameter ``lmbda``. The method also accepts
``evaluation_data``, usually either the validation or test
data. We can monitor the cost and accuracy on either the
evaluation data or the training data, by setting the
appropriate flags. The method returns a tuple containing four
lists: the (per-epoch) costs on the evaluation data, the
accuracies on the evaluation data, the costs on the training
data, and the accuracies on the training data. All values are
evaluated at the end of each training epoch. So, for example,
if we train for 30 epochs, then the first element of the tuple
will be a 30-element list containing the cost on the
evaluation data at the end of each epoch. Note that the lists
are empty if the corresponding flag is not set.
"""
if evaluation_data: n_data = len(evaluation_data)
n = len(training_data)
evaluation_cost, evaluation_accuracy = [], []
training_cost, training_accuracy = [], []
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(
mini_batch, eta, lmbda, len(training_data))
print "Epoch %s training complete" % j
if monitor_training_cost:
cost = self.total_cost(training_data, lmbda)
training_cost.append(cost)
print "Cost on training data: {}".format(cost)
if monitor_training_accuracy:
accuracy = self.accuracy(training_data, convert=True)
training_accuracy.append(accuracy)
print "Accuracy on training data: {} / {}".format(
accuracy, n)
if monitor_evaluation_cost:
cost = self.total_cost(evaluation_data, lmbda, convert=True)
evaluation_cost.append(cost)
print "Cost on evaluation data: {}".format(cost)
if monitor_evaluation_accuracy:
accuracy = self.accuracy(evaluation_data)
evaluation_accuracy.append(accuracy)
print "Accuracy on evaluation data: {} / {}".format(
self.accuracy(evaluation_data), n_data)
print
return evaluation_cost, evaluation_accuracy, \
training_cost, training_accuracy
def update_mini_batch(self, mini_batch, eta, lmbda, n):
"""Update the network's weights and biases by applying gradient
descent using backpropagation to a single mini batch. The
``mini_batch`` is a list of tuples ``(x, y)``, ``eta`` is the
learning rate, ``lmbda`` is the regularization parameter, and
``n`` is the total size of the training data set.
"""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
"""Return a tuple ``(nabla_b, nabla_w)`` representing the
gradient for the cost function C_x. ``nabla_b`` and
``nabla_w`` are layer-by-layer lists of numpy arrays, similar
to ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# backward pass
delta = (self.cost).delta(zs[-1], activations[-1], y)
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# Note that the variable l in the loop below is used a little
# differently to the notation in Chapter 2 of the book. Here,
# l = 1 means the last layer of neurons, l = 2 is the
# second-last layer, and so on. It's a renumbering of the
# scheme in the book, used here to take advantage of the fact
# that Python can use negative indices in lists.
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def accuracy(self, data, convert=False):
"""Return the number of inputs in ``data`` for which the neural
network outputs the correct result. The neural network's
output is assumed to be the index of whichever neuron in the
final layer has the highest activation.
The flag ``convert`` should be set to False if the data set is
validation or test data (the usual case), and to True if the
data set is the training data. The need for this flag arises
due to differences in the way the results ``y`` are
represented in the different data sets. In particular, it
flags whether we need to convert between the different
representations. It may seem strange to use different
representations for the different data sets. Why not use the
same representation for all three data sets? It's done for
efficiency reasons -- the program usually evaluates the cost
on the training data and the accuracy on other data sets.
These are different types of computations, and using different
representations speeds things up. More details on the
representations can be found in
mnist_loader.load_data_wrapper.
"""
if convert:
results = [(np.argmax(self.feedforward(x)), np.argmax(y))
for (x, y) in data]
else:
results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in data]
return sum(int(x == y) for (x, y) in results)
def total_cost(self, data, lmbda, convert=False):
"""Return the total cost for the data set ``data``. The flag
``convert`` should be set to False if the data set is the
training data (the usual case), and to True if the data set is
the validation or test data. See comments on the similar (but
reversed) convention for the ``accuracy`` method, above.
"""
cost = 0.0
for x, y in data:
a = self.feedforward(x)
if convert: y = vectorized_result(y)
cost += self.cost.fn(a, y)/len(data)
cost += 0.5*(lmbda/len(data))*sum(
np.linalg.norm(w)**2 for w in self.weights)
return cost
def save(self, filename):
"""Save the neural network to the file ``filename``."""
data = {"sizes": self.sizes,
"weights": [w.tolist() for w in self.weights],
"biases": [b.tolist() for b in self.biases],
"cost": str(self.cost.__name__)}
f = open(filename, "w")
json.dump(data, f)
f.close()
#### Loading a Network
def load(filename):
"""Load a neural network from the file ``filename``. Returns an
instance of Network.
"""
f = open(filename, "r")
data = json.load(f)
f.close()
cost = getattr(sys.modules[__name__], data["cost"])
net = Network(data["sizes"], cost=cost)
net.weights = [np.array(w) for w in data["weights"]]
net.biases = [np.array(b) for b in data["biases"]]
return net
#### Miscellaneous functions
def vectorized_result(j):
"""Return a 10-dimensional unit vector with a 1.0 in the j'th position
and zeroes elsewhere. This is used to convert a digit (0...9)
into a corresponding desired output from the neural network.
"""
e = np.zeros((10, 1))
e[j] = 1.0
return e
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))
卷积神经网络
对于尺寸较小图像进行简单的分类处理时,传统神经网络架构已基本足够,将每个像素亮度视为一个独立特征,并直接作为全连接网络的输入即可。但当处理分辨率较高的图像(如现代手机常见的百万像素级图像)时,网络规模将急剧膨胀,第一层全连接神经元可能多达数千万甚至上亿个。虽然可以通过图像模糊或降采样来降低计算负担,但这往往伴随着关键信息的损失。
有没有办法在尽可能保留图像信息的同时,减少计算量与模型参数?卷积神经网络(Convolutional Neural Network, CNN)正是为解决这一问题而设计的。
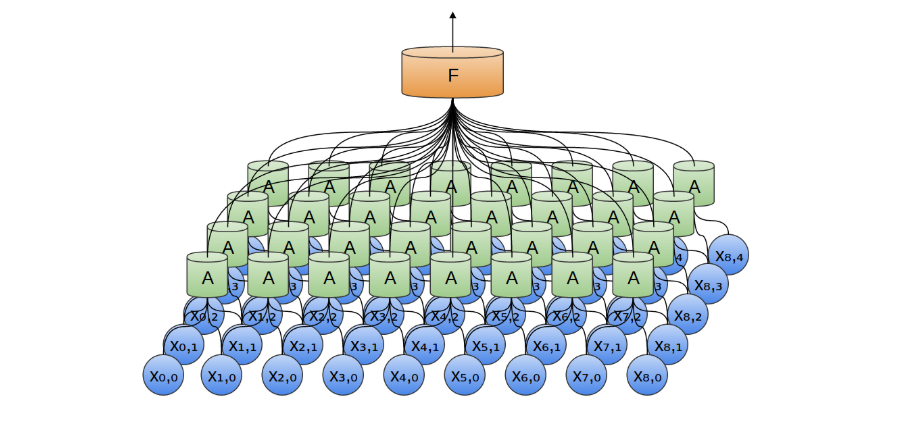
局部视野和权重复用是卷积神经网络设计核心思想。卷积神经网络(CNN)在结构上可以构建出庞大的拓扑网络,同时其待训练的实际参数数量仍可保持在相对较低的水平。
我们以一维音频数据为例来说明卷积神经网络的构造过程(该方法易于推广至高维数据)。 假设我们的目标是将音频转化为文字,最直接的做法是将音频序列作为输入,全部连接至一个全连接层进行处理。全连接层由多个神经元组成(此处简化为单一节点 F ),每个神经元与输入序列中的所有数据点相连。
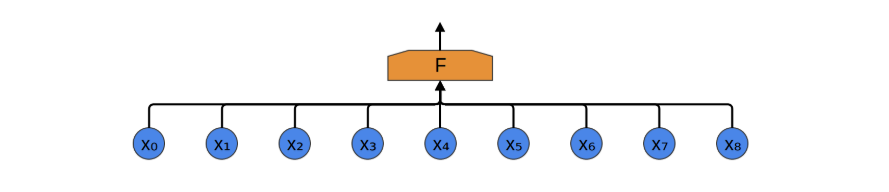
音频数据通常具有明显的局部性特征(图像数据亦然)。以“你好”为例,其对应的音频信号主要由与该词相关的局部时间片段决定,与前后语句的关联较弱。换言之,即使仅观察包含“你好”的局部音频片段,也能够准确识别其含义,且这一识别过程与该片段在整体音频序列中的具体位置无关。
因此,我们可以构建一组神经元 𝐴(在本文中定义为卷积神经元,包含多个卷积核,卷积核可视为一种滤波器,每个卷积核都可以用来匹配某种数据结构),用于局部处理输入数据的某一小段。并且,同一个卷积神经元 A 可重复应用于整个输入序列的不同位置,所有 A 共享相同的参数(卷积核),都命名成 A 就是表明,虽然卷积神经元 出现在卷积层的不同地方,但是参数是一样的(注意与全连接层对比理解,全连接层同一层的神经元的参数是不一样的!)。
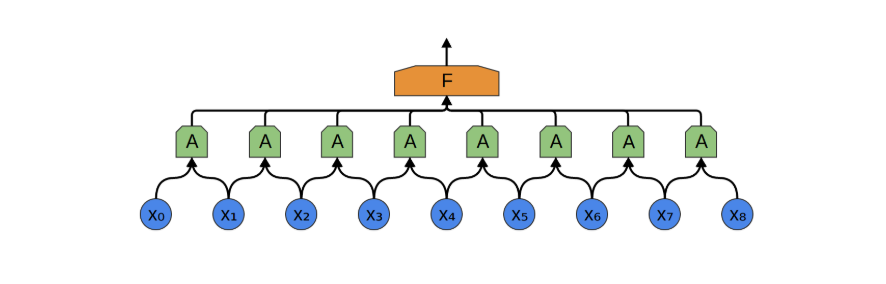
为什么能够复用?音频中的数据有某种平移不变性,比如一段音频中任意位置中关于 "你" 的数据都应该具有相似性,这和它出现的位置无关,与前后的发音无关。那么同一个卷积核,应该能识别不同位置的相似性的音频。
如果我们接受了这个设定,那么卷积神经元中的卷积核宽度(即感受野的大小)应该设为多少呢?直观上,它应当足以覆盖一个最小的语音识别单元,例如一个汉字的发音长度。然而,由于语速可能因人而异、语境不同而变化,同一个字在不同语境下持续时间可能会有较大差异,这就带来了设计上的挑战。
另一个问题是,卷积核数量应该设为多少(通道数)?是否应为每种可能的发音分配一个卷积核?举例来说,如果我们希望系统能够区分约 5000 个不同汉字的发音,是否意味着需要设计 5000 个不同的卷积核?
思考这些问题,可以帮助我们从直觉上理解 CNN,但实际情况可能不是这样的,比如识别的可能只是拼音字母的发音,或者一些不能用人的思维理解的结构。
经过卷积操作后每个卷积神经元 A可以输出多个值(注意一个卷积核一个值),单一卷积核的所有输出融合在一起是某种特征映射,特征映射可以用向量空间的投影来理解,相当于是原来数据的某个方向的投影,不同的卷积核就是不同的基向量。

如果我们卷积神经元包含 10 个卷积核,那么就能提取 10 个不同的特征映射。
我们在构造 CNN 时, 卷积层也可以叠加。你可以将一个卷积层的输出输入到另一个卷积层。通过每一层,网络都可以检测更高级别、更抽象的特征(可以理解为把一个个字,变成词,再变成短语)。
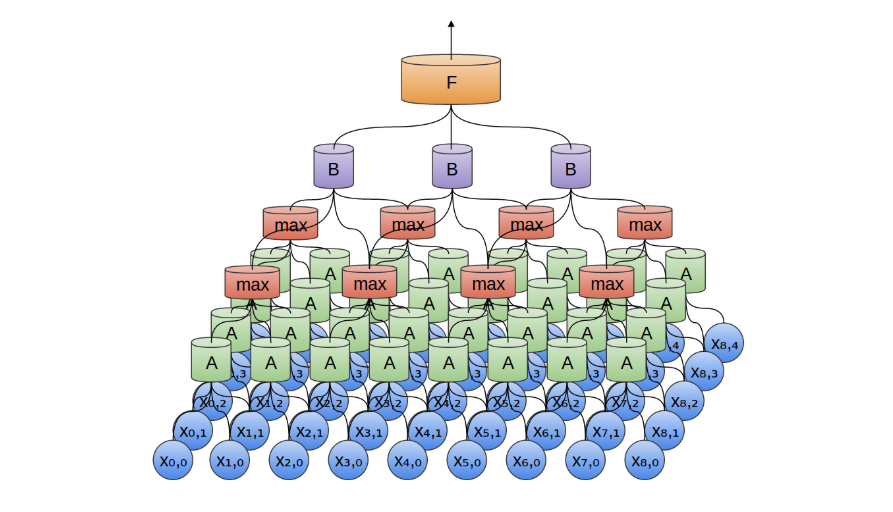
下层的多个卷积核会对上层多个卷积核的输出进行分别卷积,通常每个卷积核只会保留一个输出,最简单的操作就是平均。

原始数据经过带有多个卷积核的卷积层处理后,通常会生成比原始输入更庞大的特征表示。若直接将这些特征传递至全连接层,参数数量将显著增加,违背了我们初衷中压缩参数的目标。为此,引入 池化层(Pooling Layer)对数据进行下采样和压缩,是常见且有效的做法。
卷积层与池化层通常交替堆叠使用。池化的核心思想是:从局部区域中提取代表性信息,同时减小特征图尺寸,降低后续计算成本。更重要的是,从任务角度看,我们通常并不关心某一特征精确出现的时间(或位置),只关心它是否出现过。这使得池化在实际应用中非常合理。
以最大池化(Max Pooling)为例,它在上一层特征图的局部区域内选取最大值,作为该区域的代表。这一操作本质上回答了一个问题:“该区域中是否出现过某个重要特征?例如,一个汉字的发音特征可能在多个相邻位置被卷积核激活,其中多数是冗余甚至是噪声,通过最大池化可以提取出最强响应,
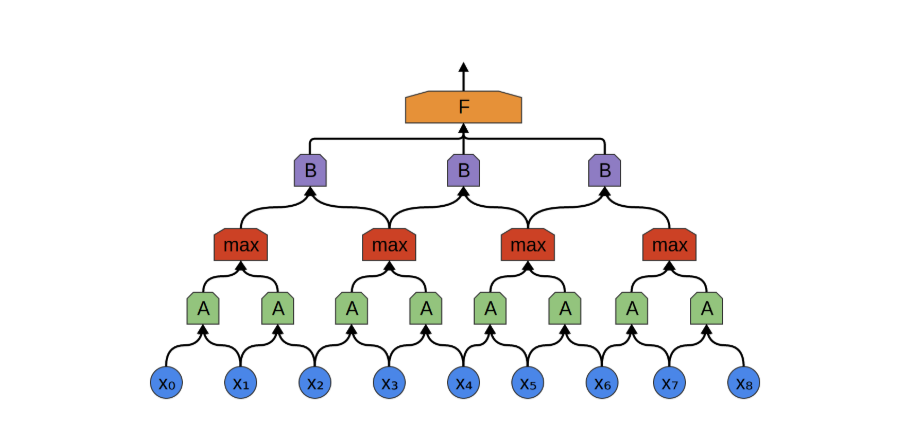
卷积层结构非常容易从一维数据推广到高维数据。卷积神经网络最具代表性的成功案例之一正是在图像识别领域的广泛应用。
在二维卷积层中,卷积神经元 𝐴 不再是沿一维序列滑动、查看片段,而是沿二维图像扫描局部区域块。对于每一个图像块,卷积神经元会提取其中的局部特征,比识别如边缘(如水平/垂直边)、纹理结构(如重复图案)、颜色变化或局部形状模式等低层视觉特征。
我们也可以在二维空间中进行最大池化。归根结底,当我们考虑整幅图像时,我们不必关心边缘的精确位置,精确到像素。只要知道边缘在几个像素以内的位置就足够了(当然可以推广到三维的情况)。
二维卷积层(池化层同理)的输出通常是二维特征图;若使用多个卷积核,其输出将成为一个三维张量(高 × 宽 × 通道数)。而全连接层的输入要求是一维向量,因此在进入全连接层前,需要通过扁平化层(Flatten Layer)将三维数组转换为一维向量。
例如,大小为 5×5×2 的数组会被转换为一个长度为 50 的向量。此前的卷积与池化层负责从输入图像中提取局部与全局特征,而全连接层则负责对这些特征进行整合与最终分类。
在分类任务中,输出层通常采用 Softmax 函数,将网络输出映射为一个概率分布,用于表示输入图像属于各个类别的可能性。由于 Softmax 的输入为一维向量,因此扁平化操作是卷积网络连接至全连接分类层的关键步骤。
卷积数学的描述
卷积的数学定义是
\[ f*g(c) = \sum_{a}(f(a) \cdot f(c-a)) \]
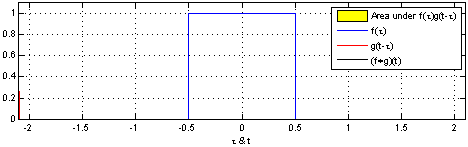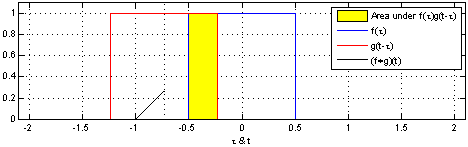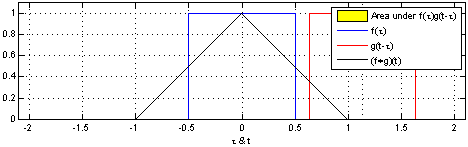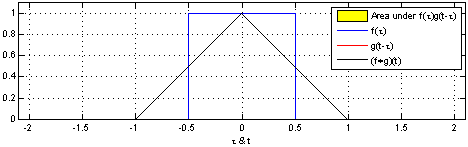
用概率的方式去理解比较容易,两个骰子和的概率,就是典型的卷积过程。 当然,\( a, b, c \) 也可以是向量,这样很容易延展到高维。
我们可以将图像视为一个二维的离散函数,每个像素对应函数在某个点的取值;而卷积核则可看作另一个函数,其值集中在较小的局部区域(其实图片也是一样的,只是稍微大点)。在卷积神经网络(CNN)中,所谓“卷积”操作,本质上是输入图像与卷积核之间的二维离散卷积。该运算通过滑动卷积核窗口,对图像的局部区域进行加权求和,从而提取出局部特征信息。
在对图片进行卷积时存在定义域问题(图片外的离散个点是否应该有意),一种常见做法是将图像边界以外的区域视为零,这种填充方式称为 零填充(zero padding)。当使用足够的填充,使得卷积输出尺寸大于或等于原图像尺寸时,该操作在数学上对应于所谓的 full convolution(全卷积)。
注意我们用离散的坐标,来描述图片的卷积过程。
原来的图片 \[ P(i, j) = p_{i, j} \qquad N \ge i \ge 0, M \ge j \ge 0\]
卷积核,注意 i 和 j 只在很小的范围(比如 k=3) \[ H(i, j) = w_{i, j} \qquad k \ge i \ge 0, k \ge j \ge 0 \]
其中 \( w = \{ w_{i, j} \} \) 就是卷积核的权重系数。
卷积之后的二维数据为
\[ G(n, m) = P * H (n, m) \sum_{i, j} P(i, j) \cdot H(n-i, m-j) \]
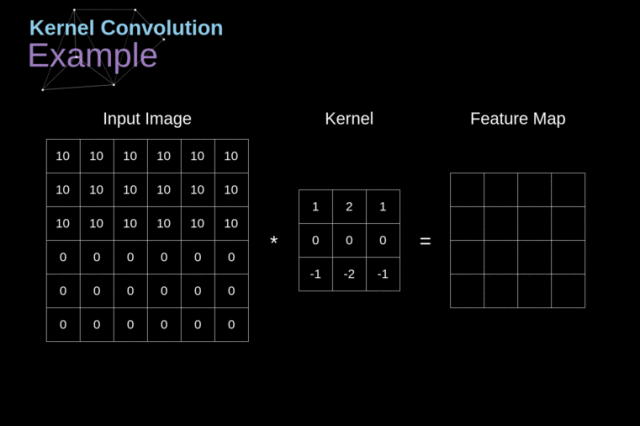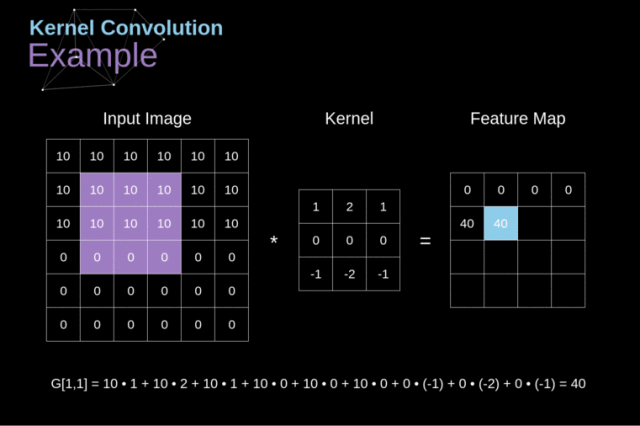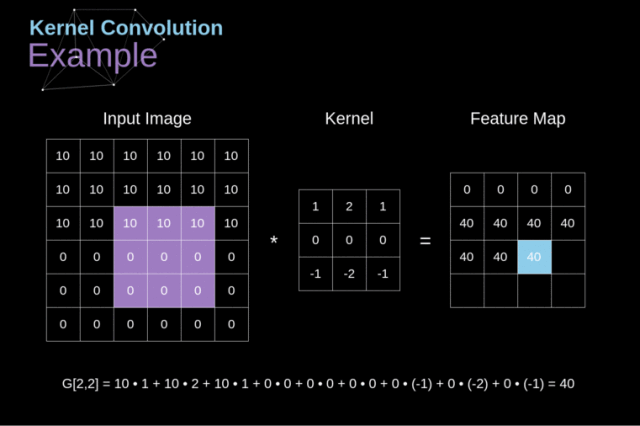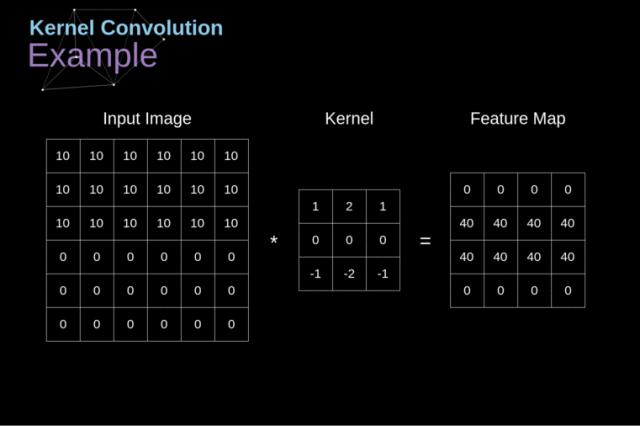
上图展示的就不是全卷积,我们每次卷积之后,数组变小了(图片的定义域限制了卷积后的坐标值)。
在实际的卷积神经网络中,卷积神经元是具有多个卷积核,也就是说有多个 \( w^k \),每个权重系数组\( w^k \),可以理解为一种滤波器。

我们可以人工设计一些卷积核(赋予一些有意义的权重),比如用卷积核寻找边缘 ,来看看在整张图上执行卷积运算之后得到的结果:

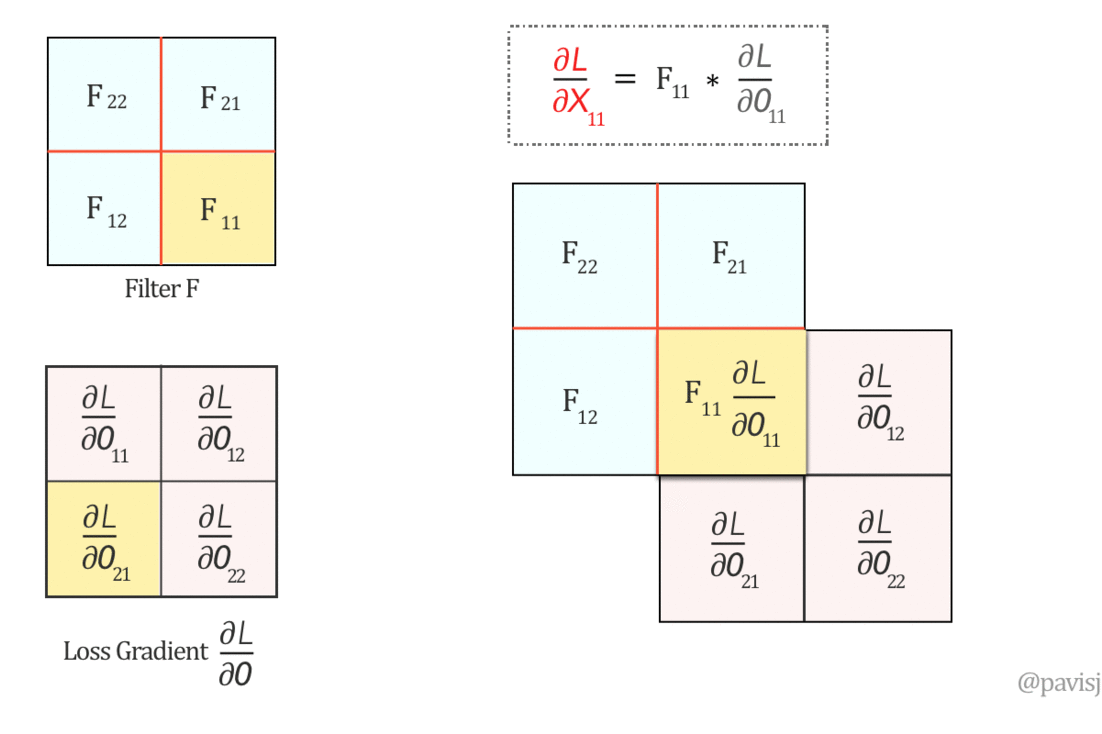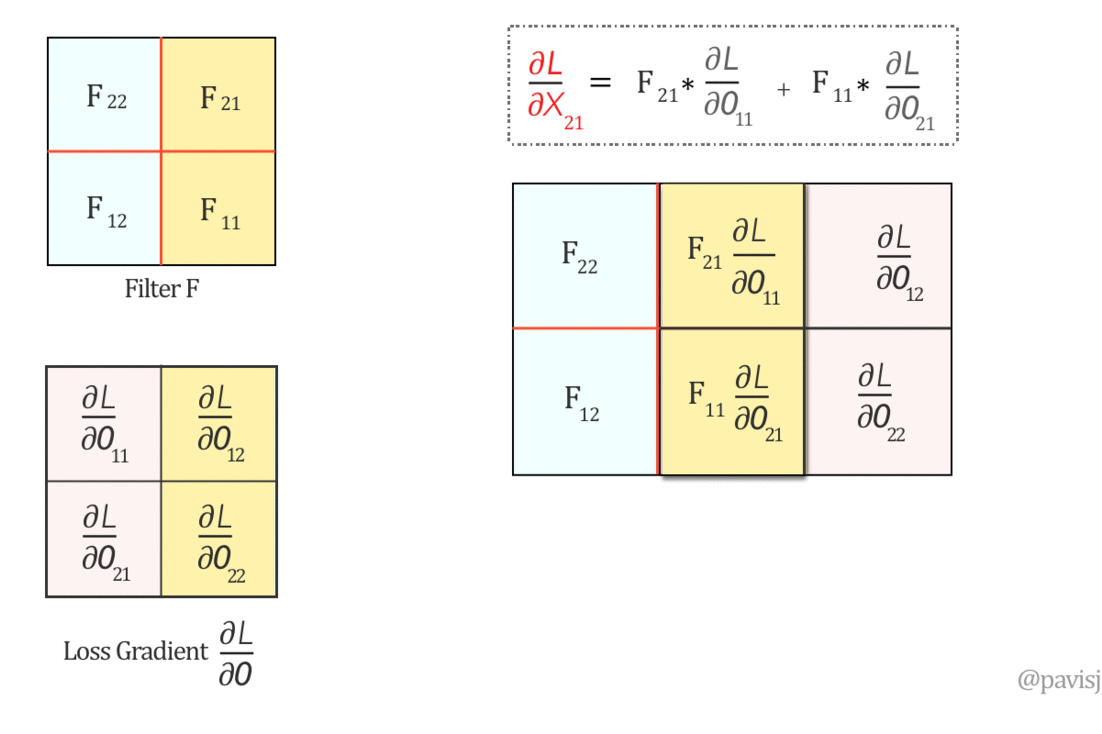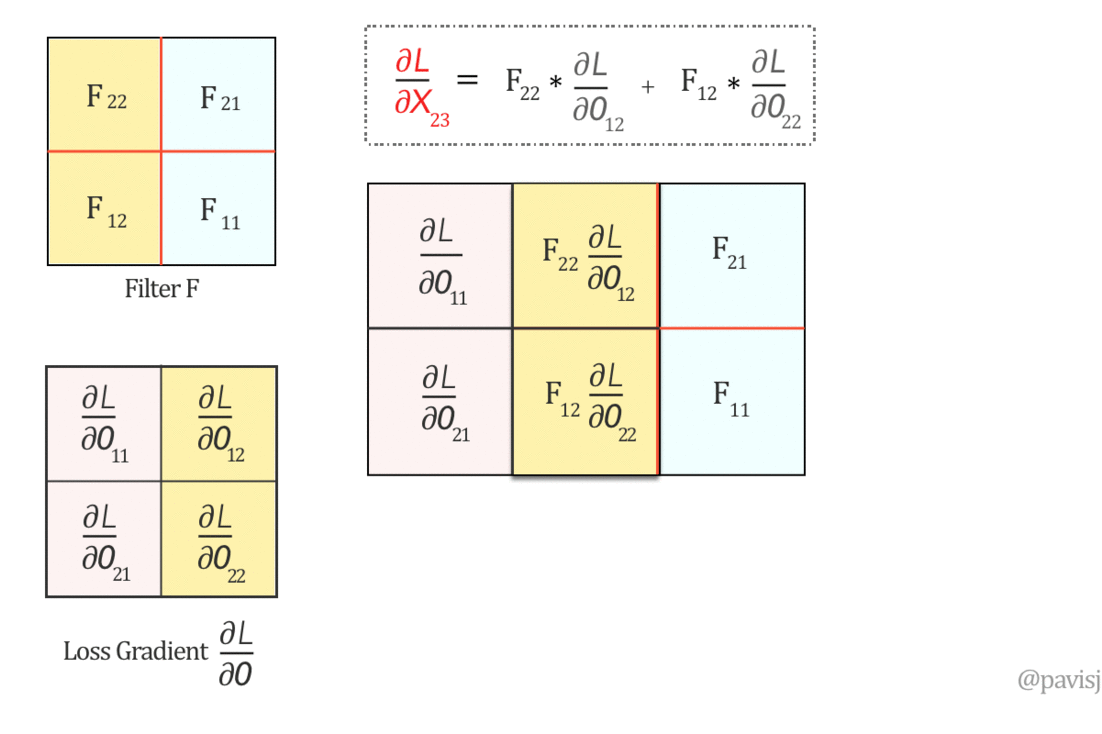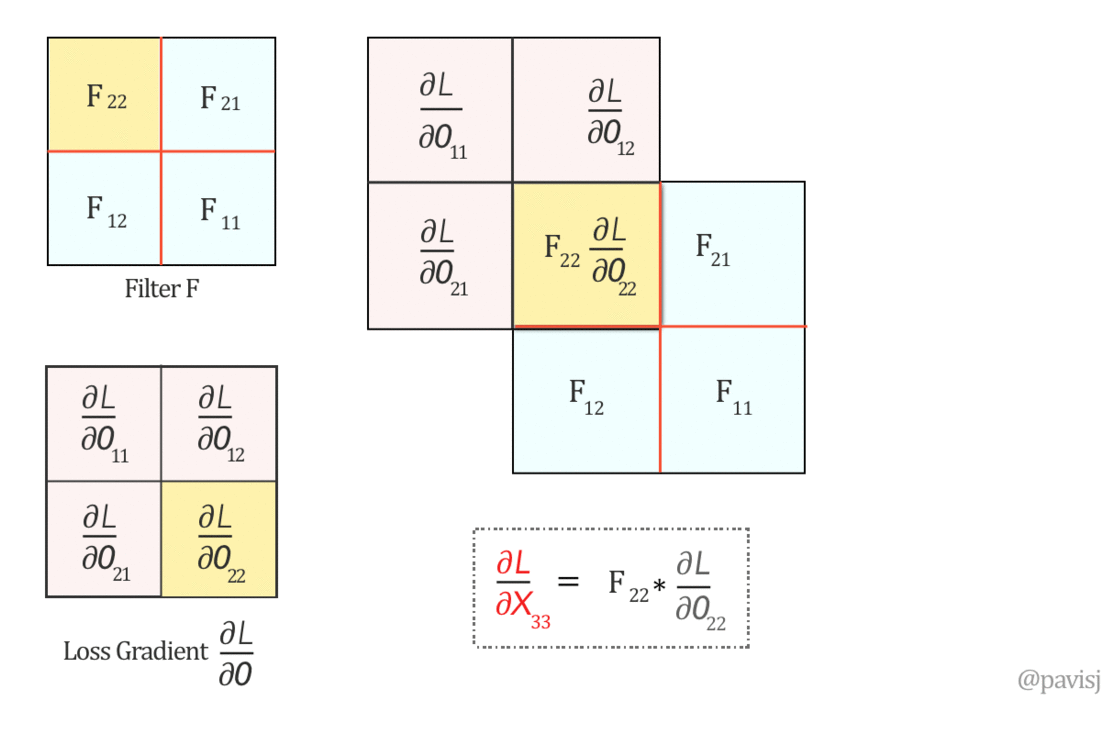
反向传播
对于一个卷积核,其权重的更新是,该卷积核的输入 与 下一层反向传播回来的误差函数的梯度的卷积(卷积核就是这个误差函数梯度矩阵)。
\[ \frac{\partial G^l}{\partial W^l} = CONV \:(y^{l-1}, \frac{\partial C}{\partial G^l})\]
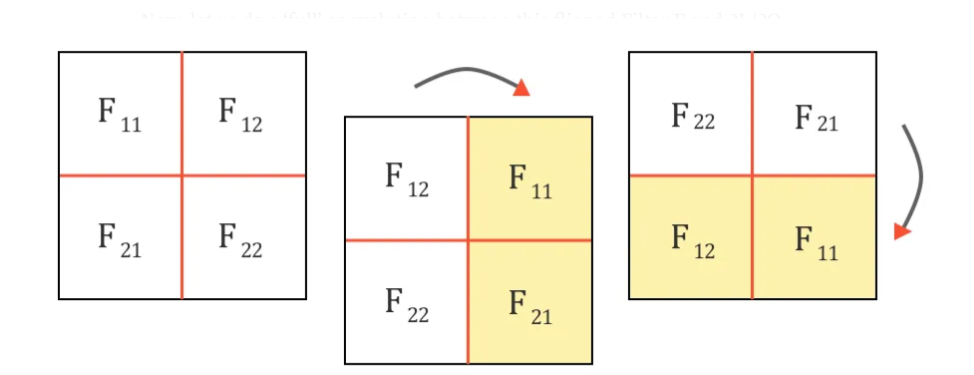
而需要传递到上一层的误差函数梯度,可以表示 为 180 度旋转(先垂直翻转,再水平翻转)的卷积核权重,与下一层反向传播回来的误差函数的梯度的卷积。
\[ \frac{\partial C}{\partial y^{l-1}} = Full \; CONV \:(180^o 旋转 W^l, \frac{\partial C}{\partial G^l}) \]
ResNet
ResNet(Residual Neural Network)是一种深度卷积神经网络,由 Kaiming He 等人于 2015 年提出,用于解决深层神经网络训练中的退化问题。其核心思想是通过残差连接引入恒等映射,使得网络更容易训练。
传统的前馈网络结构中,每一层的输出为:
\[ \mathbf{y} = \mathcal{F}(\mathbf{x}, {W_i}) \ \]
其中,$\mathbf{x}$ 为输入,$\mathcal{F}$ 为非线性映射函数。
而在 ResNet 中,加入了恒等映射:
\[ \mathbf{y} = \mathcal{F}(\mathbf{x}, {W_i}) + \mathbf{x} \]
其中:
- \(\mathcal{F}(\mathbf{x})\) 表示残差部分(如两层卷积 + ReLU),
- \(\mathbf{x}\) 是 shortcut connection(跳跃连接)的输入,
- 这样可以让网络学习残差 \(\mathcal{F}(\mathbf{x})\),而不是完整的映射。
在做残差连接时,需要处理维度对齐的问题。
从优化角度看,残差连接将目标函数从直接学习 \(H(x)\) 转换为学习 \(F(x) = H(x) - x\),更容易优化:
\[ H(x) = F(x) + x \]
当最优映射接近恒等映射时,残差学习的目标 $F(x) \approx 0$,更加稳定。
循环神经网络
对于传统的神经网络,在进行前向计算时,各次调用之间是相互独立的。例如,对两张图片进行分类时,第一次的分类结果不会影响第二次的识别过程,二者是完全分离的运算。因此,这类神经网络通常要求输入的维度保持完全一致。
然而,有些任务的输入维度并不固定。例如,提取一句话中与时间相关的描述时,不同句子所包含的词数往往不同,这就带来了输入长度不一致的问题。对此,常见的一种解决方法是“补齐”,即将所有句子强制调整为相同的长度:不足的部分用空白填充,超出的部分则予以截断。这种方法虽然简单直接,但显得不够优雅。
另一种思路是将任务切分为一致的最小输入单元,例如逐字处理。基于此,可以设计一种神经网络,使其每次仅处理一个字,同时通过某种机制将前一次处理得到的信息传递到当前步骤,从而在保持输入长度灵活性的同时,实现上下文之间的关联。
循环神经网络(Recurrent Neural Networks, RNN)很好地解决了输入维度不一致的问题。RNN 的结构中引入了循环机制,使得网络能够在时间维度上传递和保留信息(这里的时间维度,只是一种顺序而已)。
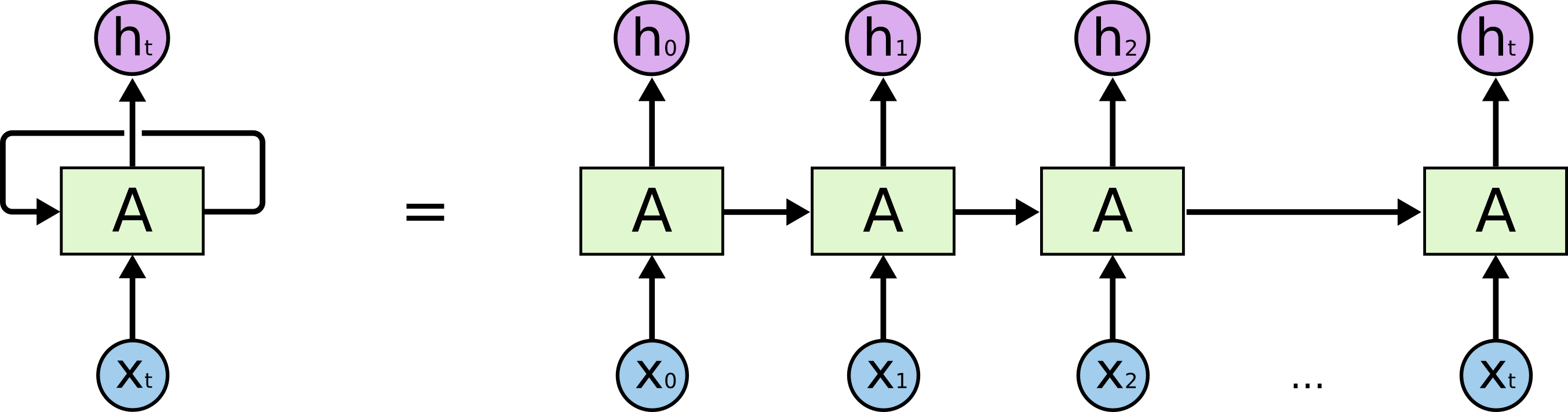
循环神经网络最核心的思想是延展输入向量(不仅仅看现在的词,还要看上文),同时输出一个前文压缩信息给后续的调用使用(上文哪里来? 一种标准的网络结构在存储上文信息)。
循环神经网络应用很广法,这些成功的关键在于使用了“LSTM”,一种非常特殊的循环神经网络,它在许多任务中比标准版本表现得好得多。几乎所有基于循环神经网络的令人兴奋的结果都是通过它们实现的。正是这些 LSTM 将是本文探讨的内容。
LSTM 的数学表达式
一个 LSTM 神经元 相当于四个普通神经元。
输出神经元(和普通的神经网络没区别,只是扩展了上下文) \[ o_t = \sigma(W_o x_t + U_o h_{t} + b_o) \]
输入神经元 \[ i_t = \sigma(W_i x_t + U_i h_{t} + b_i) \]
遗忘神经元 \[ f_t = \sigma(W_f x_t + U_f h_{t} + b_f) \]
记忆神经元 \[ c_t = f_t \otimes c_{t-1} + i_t \otimes \sigma(W_c x_t + U_c h_{t} + b_c) \]
隐藏状态 \[ h_{t+1} = o_t \otimes \sigma(c_t) \]
其中,\( h_0 = 0 \)
LSTM 神经元可以横向排列,组成 LSTM 层。不同的神经元可以从输入序列中提取上下文信息的不同方面,从而实现更丰富的特征表示。
关于训练
训练用时间反向传播,还是利用链式求导法则进行推导,与一般的神经网络不同,其梯度来源不仅仅是某一个网络的调用,还来来至后一次某一个网络的调用传到的输入向量的梯度(\( h_t \))。
循环神经网络的训练数据是 \( k\) 个输入输出对的有序序列。
\[ <x_0, y_0>, <x_0, y_0> ... \]
首先按顺序前向运行一个循环神经网络,运行后的神经网络包含 \( k\) 个输入和输出。
\[ <x_0, h_0 , \hat{y}_0, h_1>, <x_1, h_1, \hat{y}_1, h_2> ... \]
但每个网络副本都共享相同的参数。然后,使用反向传播算法求出损失函数相对于所有网络参数的梯度。
embedding
字符的原始编码(比如,UTF-8)的设计目标是将不同的字符区分开(当然会考虑兼容性和存储效率问题),并不适合用于字符的意义判断,比如是否相似(中文字符),如何组成一个有意义的词(比如,英文单词)。
因此,我们需要将字符串编码成便于后续计算的数据(一般用向量来做),主要任务有以下几个。
- 将字符串分成一个个小片段(最小的,有意义的片段)。
- 将这些片段表示为一个向量。
这个过程要做 embedding,embedding之后的数据叫做 token,英文单词比较多,一般不会为每个单词都生成token,而是进行分词切片(子词),一个单词因为不同的形态会产生不同的词,如由look衍生出的look, looked,显然这些词具有相近的意思,但是在词表中这些词会被当作不同的词处理,一方面增加了冗余,另一方面也造成了大词汇量问题。
分词字词之后,单词中止符也会被作为一个单独的子词。这样解码的时候,就很容易进行,如果相邻子词间没有中止符,则将两子词直接拼接,否则两子词之间添加分隔符。
再一次大模型调用钟,首先我们要把用户的输入(问题) string 进行切片,切片之后叫做 token,有可能是单词,也有可能只是单词的片段(to, world, meta...),对于视频和图片而言,tokens可能代表一小块图片或者一小段语音,而每个token对应一个向量,也就是一组数字。
\[
to = \begin{bmatrix}
1.2 \
0.1 \
0.3 \
... \
2.3
\end{bmatrix}
\]
我们把这个过程叫做 Embedding。
\[ vector = Embedding(token) \]
如何构建Embedding,我们的目标是要让该向量,代表字符的意义(向量就是意义),这种向量可以想象为高维空间的点,字符(token)之间越相似,那么向量在空间中就会越接近。
\[E(雌) \approx E(雄) + E(女) - E(男)\]
那么如何编码token的?又是如何确定维度的(GPT-3有12288个维度)?
模型有预设的词汇库(~50k),Embedding Matrix,就是每个词都对应一个向量。
Transformer
Transformer 的核心思想是通过自注意力机制(Self-Attention)和多层堆叠的神经网络进行语言建模。
先不管这些高大上的算法词汇,先用技术上宏观梳理数据流, 那么,基于 Transformer 构建文本生成的核心数据流是什么?
输入是一个字符串,比如'北京位于',输出这是这个字符串后可能的字的概率,比如 '北':20%,'京': 10%。
如何做到求概率,第一步当然是量化这些字符。
有了数字,才能做计算。
一个输入字符串,\( [北, 京, 位, 于] \) 会被描述为一个二维的数组(上下文长度,GPT: 2048)。
接着输入到注意力机制模块模型中,该模型允许向量(token)之间进行相互约束,来重新更新每个向量,
为什么要这么做,因为一个词在不同的语境下应该有不同的含义(*含义就是向量)。比如 问问题 中的两个 问显然不是一个意思,
因此需要根据上下文,更新向量,也就是说,上下文的向量会拉扯当前的向量,使得它指向新的方向。
然后将更新后的每个向量,输入到多层感知机中,向量之间没关系,这是在提取每个字符本身的含义(这是中文吗,这是一个动词吗?这是数字吗?输出的维度暗含了我们考虑的方面有多少)。
然后重复之前的过程
Attention -> Preception -> Attention -> Preception -> ... ->
最后的目的,是将整个字符串的所有关键含义在最后一个向量中表达出来。
然后再对最后一个向量作为输入,与Unembedding Matrix相乘(类似每一个词与最后一个向量的相识度), 再进行归一化处理,得到所有token的概率分布。
\[ W_U \times x_{out} = y_{out}\]
自注意力机制
那么什么是自注意力机制?
多层堆叠的神经网络
扩散模型
从自编码开始
降维可以看作是一种有损压缩(特殊情况下也可以是无损的)。当我们希望减小图片大小时,就可以采用降维技术。
例如,一些线性变换技术(如傅里叶变换、小波变换),本质上就是对数据进行换基操作。通过将数据表示在一组新的标准正交坐标系下,可以使得信息更加集中于少量的维度上,从而只需存储有限的元素值即可还原大部分信息(为什么可以做到这一点?因为数据本身存在一定的结构和规律,例如周期性或大面积纯色背景,此时其信息熵较小,具备较高的可压缩性)。比如一张 1000×1000 像素的图像,其原始维度为 1000²;如果采用傅里叶变换进行换基,可能仅通过前 1000 个较大的系数值,就能将图片还原到与原图相似度达 99.9%,此时的压缩比约为 1/1000。
在数据分析中,我们同样会用降维方法,比如主成分分析(PCA)。那么,为什么要在分析中使用降维?主要目的是提取数据的核心特征(也就是说数据的信息熵较小,存在较大的压缩空间)。通过分析少量关键维度的变化(向量的前几项),我们就能较为准确地描述数据的主要特征(所谓“描述主要特征”,其实就是用有限数量的特征,尽可能还原原始数据的变化趋势。虽然无法做到 100% 还原,但可以保留大部分的数据特性)。
无论是在数据压缩中,还是在数据分析中的降维任务,其背后都遵循类似的技术结构,那就是自编码器(Autoencoder, AE)。
- 编码器(压缩):\( z = f(x) \in \mathbb{R}^d \)
- 解码器(还原):\( \hat{x} = g(z) \approx x \in \mathbb{R}^N\)
编码器和解码器要受到一个约束,就是数据信息尽量不要损失,也就是损失函数最小。
\[ \mathcal{L}_{\text{AE}}(x) = | x - \hat{x} |^2 \]
我们也可以将自编码器看作是一个函数形式:
\[ x = F(x) \]
它本质上是一个从自身到自身的映射函数。
如果单从这个函数形式来看,似乎没有太大意义——既然我们已经知道了 𝑥,为什么还要通过函数再“求”一遍自己?但如前所述,自编码的核心意义在于我们关注的是这个函数中的中间参数表示,通过这个中间表示可以实现有效的压缩。
从自编码的函数形式 \( x = F(x) \) 出发,我们会发现,神经网络结构本身就天然具备自编码器的特征。其中的隐藏层输出(在很多语境中也被称为“特征”)就是我们所需要的压缩后的向量表示。
在实际应用中,当我们对数据进行降维处理后,有时会尝试为新的维度赋予一定的物理意义(例如:短期波动、日变化、长期趋势等)。但在大多数情况下,这些压缩后的向量维度是很难直接与现实世界中的具体含义对应起来的。
然而,无法明确解释每个维度的含义,并不妨碍我们以这种方式去理解降维的结果。我们可以假设这些维度潜在地代表了一些语义特征。比如,图像经过降维压缩后,不同的向量维度可能隐含着“周期性强”“背景纯色”“风格偏卡通”等抽象属性。
在神经网络中实现自编码器时,我们通常将其结构划分为两个部分:编码器(Encoding) 和 解码器(Decoding)。
- 编码器:\( z = f(x) \in \mathbb{R}^d \)
- 解码器:\( \hat{x} = g(z) \approx x \in \mathbb{R}^N\)
基于神经网络构建的自编码器不仅可以实现降维(压缩),它其实也可以被推广用于升维(扩展)。有时候,我们并不是希望简化原始数据的维度,而是希望从更多的角度、在更高维的空间中去描述和理解它。
举个例子,我们知道一个中文词语在 UTF-8 编码下通常由两个字符组成,也就是大约 32 位(可以看作一个整数)就可以表示。但如果我们希望从更丰富的语义层面去理解这个词,就不再满足于这种紧凑编码。我们可能会关心:这个词是不是一个人名或地名?它是否具有积极的情感倾向?是否属于动物类词汇?
这些语义信息不能从原始 UTF-8 编码中直接获得,但通过升维的方式,我们可以将一个原始的低维数据(例如一个整数或字符编码)映射到一个更高维的向量空间,在这个空间中,每个维度都可能对应某一类特征的“存在性”或“相关性”。
因此,自编码器不仅能用于压缩数据,提取核心特征,还可以通过适当设计结构或目标函数,用于扩展数据的表达能力,从而使得机器更全面地“理解”数据的语义内涵。
有了上面的理解,我们可以进一步思考一个问题:当我们拥有一个基于神经网络构建的自编码器的解码器(Decoder)部分时,如果我们不再通过输入 𝑥 得到压缩向量 𝑧 ,而是直接生成一个向量(比如随机采样),那么这个向量经过解码器输出的结果是否依然是有意义的?也就是说,假设我们跳过编码器这一步,直接手动或随机生成一个向量 𝑧,然后将其输入解码器(这就是生成模型):
\[ \hat{x} = g(z) \]
那么这个 \( \hat{x} \) 是否还能保持一定的结构性或语义上的合理性?如果这个向量是“合理地”采样的,答案是:有可能。
举个例子,如果我们想生成一张图片,而输入给解码器的向量并不是通过真实图片编码得到的,而是基于某种语义生成的(例如我们根据一句话“快乐的狗”得到某种语义表示,或者在潜在空间中人为构造一个向量),那我们解码后能否得到一张与这句话相符的图片?
这正是变分自编码器的核心思想所在。
生成模型
了解变分自编码器前,我们先了解一下生成模型。
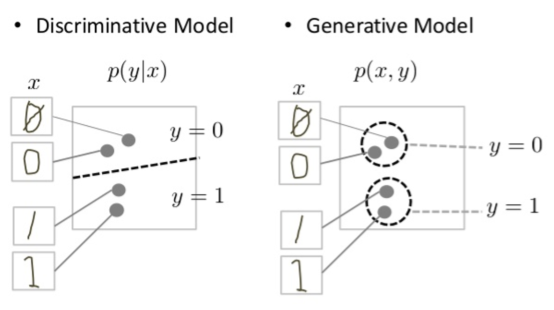
在分类应用中(离散回归),我们希望从观测 x 得出标签 y (一个图片是不是狗,今天温度是28度,那么明天的气温是不是30度?)。我们可以直接进行回归拟合,而无需使用概率分布,这类方法叫做无分布分类器;我们也可以估计给定观测的标签概率 ( p(y|x)),通过概率的最大值,得到输入特征的分类,这种叫做判别模型;或者可以预估联合分布( p(y, x)),由此计算( p(y|x)),然后以此为基础进行分类,拟合联合分布的方法叫做生成模型。这些方法越来越间接,但越来越具有概率性,从而允许应用更多的领域知识和概率论。
我们为什么要搞这么复杂,取得到一个联合概率( p(y, x))呢?,我们想要的是分类过程的逆过程(分类过程:给一张图片判别是否是狗,生成过程:帮我画一张狗的图片),也就是基于联合概率,我们可以通过 y 来生成 x(这也是生成二字的意义),也就是我们更关注的是 ( p(x|y))。如果没有标签(无监督),我们拟合的是 ( p(x)) ,通常直接给出 ( p(x)) 很困难,我们会构造一个潜变量,从而得到 ( p(x|z)) ,也就是随机采样一个z,从而生成 x 。
与判别模型相比,生成式模型要解决更难的任务。生成模型必须模拟更多。
判别模型会尝试在数据空间中划定边界(只需查找一些特征模式,即可学会区分样本),而生成式模型会尝试对数据在整个空间中的放置方式进行建模。
变分自编码器 (Variational Auto Encoders, VAE)
Variational Auto Encoders combine the approximation abilities of deep neural networks and the statistical foundations of generative models.
我们先做一个假设:压缩后的图像向量中的每个维度是具备语义的(卡通、有深林,有河流...)。即使我们随机生成一组向量数值,例如:卡通 = -0.3、有森林 = 0.3、有河流 = 0.1 ... ,这组数据虽然在数值上是随机的,但它们的维度本身不是随机的(什么叫维度不随机?如果我们从所有汉字选择汉字,生成句子,可能这个句子没有任何意义,但是如果我们固定一个句子格式,比如名称+动词+名词,那么在根据格式中的要求(维度),随机生成的这个句子,就会有点语义含义),每个维度都对应着某种潜在的语义特征(向量空间具有某种结构性),因此这个向量在每个值都随机的情况,依然能够描述了某种结构性信息。
但问题来了:如果我们把这样一个向量直接交给图像解压器(比如傅里叶逆变换)作为压缩后的表示,让解压器去生成图像,很可能生成的图像是完全没有意义的。
这是为什么?因为傅里叶变换的每个维度并不是 卡通、森林、河流这些人类语义上的特征,而是频率分量,是某种数学空间上的正交基分解。它们和语义空间之间并没有可解释的映射关系,因此随机拼凑的频率向量几乎必然会导致语义上混乱的结果。
那么,怎样才能让这个生成过程变得有意义呢?
核心思路是:我们需要一种压缩方法,使得压缩后的向量维度本身就是有语义结构的、连续可调的(最后这个才是关键)。也就是说,encoding 后的向量空间要满足两个关键条件:
- 每个维度具有潜在语义(或语义可解释性)
- 维度值是连续的,能够支持在语义之间进行插值(训练)或采样(预测)
这正是 变分自编码器 所提供的解决方案之一。
VAE 在传统自编码器的基础上,引入了概率建模思想。编码器不再直接输出一个确定性的压缩向量 𝑧,而是输出一个概率分布,通常假设是高斯分布:
\[\mathcal{N}(\mu_\phi(x), \sigma_\phi^2(x))\]
什么叫输出一个概率分布? Encoding 时,我们是基于 \(x\) 得到潜变量每个维度的概率分布的参数(注意是每个维度,描述的是高维分布,也叫联合分布、多元分布),某种意义上讲,如果知道了概率分布的函数,概率分布就是概率分布的参数。
\[ \mu = \mu_\phi(x)\] \[ \sigma = \sigma_\phi^2(x) \]
那么 为什么 \(x\) 对应的是一个概率分布,有什么直觉上的认知?可以认为 参数均值 \(\mu\) 代表的就是这张图在每个语义维度的值(有多卡通? 有多动物?),而 \(\sigma\) 代表了一种维度在语义上的模糊性,也就是一个图片有多卡通 不是一个客观的评价标准,应该给一些不确定性。 而从技术的角度讲,正是由于这种概率化的不确定性,才允许我们后期在每个维度上进行随机采样。
class Encoder(nn.Module):
def __init__(self, i_dim, h_dim, z_dim):
super(Encoder, self).__init__()
self.fc = nn.Linear(i_dim, h_dim) # 增加模型复杂度,更好的映射 x-> sigma, mu
self.fc_mu = nn.Linear(h_dim, z_dim) # 输出高斯分布均值
self.fc_logvar = nn.Linear(h_dim, z_dim) # 输出高斯分布对数方差
def forward(self, x):
h = torch.relu(self.fc(x))
mu = self.fc_mu(h)
logvar = self.fc_logvar(h)
return mu, logvar
然后,我们基于 从 x 得到的分布参数,去采样一个 \(z\) (高维随机变量)。采样使用的是重参数化技术,这样做为了让神经网络的节点权重落在概率分布的参数上,从直觉上的理解,当后向传播的梯度到了 \(z\) 这个节点上,只有 \(\mu\) 和 \(\sigma\) 需要继续向后传递梯度。
\[ z = \mu + \sigma * \varepsilon \] \[ \varepsilon \in \mathcal{N}(0, 1)\]
def reparameterize(mu, logvar):
# 重参数化技巧:z = mu + exp(0.5*logvar) * epsilon
std = torch.exp(0.5*logvar)
eps = torch.randn_like(std)
return mu + std * eps
从代码上,可以更好的理解重参数化技术,如果以上函数直接写成 torch.randn_like(std, std, eps),一个随机过程怎么能求导呢?
最后对 \( z \) 进行解码,我们知道 \( z \) 是一个随机变量,同时对 \( z \) 进行解码运算生成的 \(x\) 其实也是一个随机变量,如何直观的理解这种概念? 比如生成 一只可爱的狗的图片,我们可以生成 一个输入向量 \( z_{dog} \)(可爱=1.0,狗=1.0 ...),很多种图片都能与这句话对应上(当然这类图片肯定具备一定的相似性)。
\[ \hat{x} \sim p_\theta(x|z) \]
class Decoder(nn.Module):
def __init__(self, z_dim, h_dim, o_dim):
super(Decoder, self).__init__()
self.fc1 = nn.Linear(z_dim, h_dim)
self.fc2 = nn.Linear(h_dim, o_dim)
def forward(self, z):
h = torch.relu(self.fc1(z))
x_hat = self.fc2(h) # 高斯分布假设
# x_hat = torch.sigmoid(self.fc2(h)) # 伯努利分布假设
return x_hat
# return x_hat + torch.randn_like(x_hat)*0.01 # 理论可以加上噪声,表示条件概率
我们要学习的是 隐变量的维度(每个分量都是标准正态分布)和 推断的过程 \(\hat{x} = g_\theta(z)\)。
把组件放在一起,组成训练时的前向
class VAE(nn.Module):
def __init__(self, i_dim, h_dim, z_dim):
super(VAE, self).__init__()
self.encoder = Encoder(i_dim, h_dim, z_dim)
self.decoder = Decoder(z_dim, h_dim, i_dim)
def forward(self, x):
mu, logvar = self.encoder(x)
z = reparameterize(mu, logvar)
x_hat = self.decoder(z)
return x_hat, mu, logvar
我们应该如何去学习这个这个神经网络呢?
如果我们将图片的每个像素都作为一个维度,那么一张图片就是一个高维向量(一般会把每个维度的值归一化到 0-1上)。所以每张图像 \(x\) 都是在这个高维空间(高维立方体)中的一个点,这些点在高维度的空间中非常稀疏,但是由于图片的相似性,我们有理由相信空间的某些区域会出现图片点的聚集(可以想象整个宇宙空间的恒星分布,虽然聚集,但是大部分都是真空的,图片空间的维更高,其实很难有直觉上的想象),聚集的这些点代表了某一类语义化的图片(比如快乐的狗),同时一张图片的某些像素轻微的扰动,我们基本上也会认为是描述的同样的意义(因此图片空间可以认为是连续)。
而我们关注就是空间中的点的聚集密度(注意图片空间是连续的),从概率上讲,我们给定的先验图片集(训练数据集),在图片空间分布的密度代表的是该区域出现图片的概率有多高,注意不是某个点的概率(在连续空间里,任何单个点的概率都是 0),我们的目标是知道哪些区域采集到的点为图片的概率高,因而确定采样的方向。
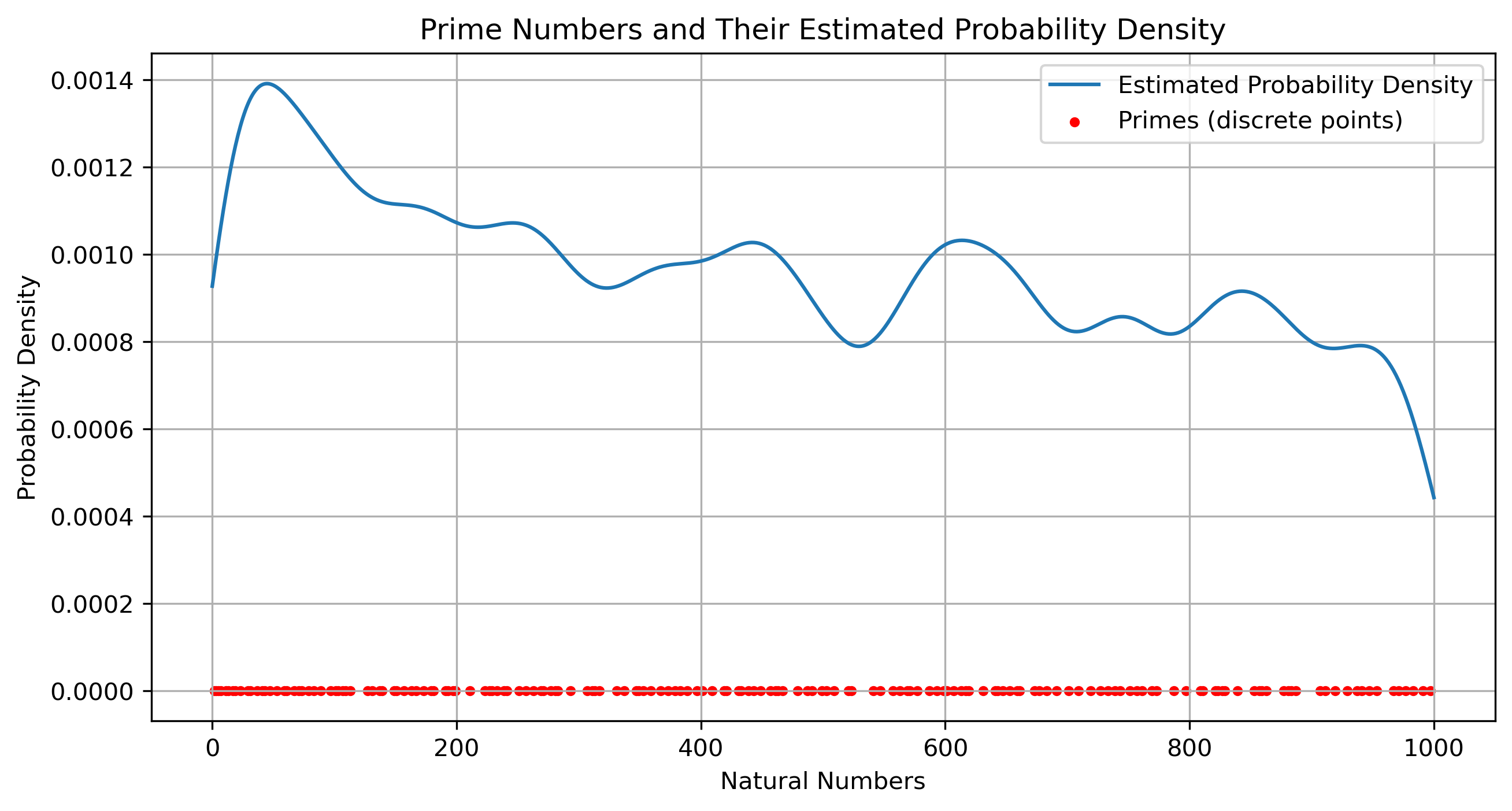
以质数在数轴上出现的概率(核密度估计来从离散质数点估算出一个连续的概率密度曲线)来类比,图片在图片空间上出现的概率(图片空间上的概率密度一定是大面积为 0 )。
- 单个质数(如 7) ⇒ 是一个点,概率为0;
- 某个区间(比如20到30) ⇒ 里面质数多 ⇒ KDE密度曲线在这里高;
- 所以连续曲线其实是在描述离散点群的密度。
真实的图片在图片空间上的概率密度函数 \(p(x)\) 是未知的,因此我们需要根据提供的图片集,找到一个 \(p_\theta(x) \approx p(x)\),来进行近似(最大似然函数),没有具体的函数形式,由于维度太高,我们也没办法,采用离散化的方式来描述,但是由于图片概率密度的稀疏性,我们可以进行概率映射(引入潜变量)。
我们对似然函数取对数(对数似然,单调递增函数,不改变极值性质),并引入一个额外的随机变量 \(z\) (潜变量,隐藏的维度),可以得到 \[ \log p_\theta(x) = \log \int p_\theta(x, z) , dz \] 这里:
- \(p_\theta(x, z) = p_\theta(x|z) q(z)\),是\(z\) 和 \(x\) 的联合分布;
- \(q(z)\) 是先验,一般设为标准正态 \(\mathcal{N}(0, I)\)。
引入变分分布 \(q_\phi(z|x)\),用一个可调的分布\(q_\phi(z|x)\),去近似一个难算的真实后验分布\(q(z|x)\),这种用可调分布近似复杂分布的方法,在数学上就叫变分推断(在函数空间里找最优函数)。
\[ \log p_\theta(x) = \log \int \frac{p_\theta(x, z)}{q_\phi(z|x)} q_\phi(z|x) , dz \]
应用期望的定义 和 Jensen 不等式(因为 \(\log\) 函数是凹函数,所以可以应用 Jensen 不等式)
\[ \log E_{q_\phi(z|x)}\left[\frac{p_\theta(x, z)}{q_\phi(z|x)}\right] \geq E_{q_\phi(z|x)} \left[\log \frac{p_\theta(x, z)}{q_\phi(z|x)}\right] \]
整理右边 \[ \log p_\theta(x) \geq E_{q_\phi(z|x)} \left[\log p_\theta(x, z) - \log q_\phi(z|x) \right] \]
用链式则展开联合分布 \(p_\theta(x, z)\)
\[ = E_{q_\phi(z|x)} \left[\log p_\theta(x|z) + \log q(z) - \log q_\phi(z|x) \right] \]
\[ = E_{q_\phi(z|x)} [\log p_\theta(x|z)] + E_{q_\phi(z|x)} [\log q(z) - \log q_\phi(z|x)] \]
后半部分就是 KL 散度的负值(KL 散度用来度量两个分布之间的相似性):
\[ D_{\text{KL}}(p | q) = \sum_{i}p(i)ln \frac{p(i)}{q(i)} \] 典型情况下,\(p\) 表示数据的真实分布,\(q\) 表示数据的近似分布(建模、拟合获得)。
根据定义可得: \[ D_{\text{KL}}(q_\phi(z|x) ,|, q(z)) = E_{q_\phi(z|x)} \left[\log \frac{q_\phi(z|x)}{q(z)}\right] \]
所以
\[ \log p_\theta(x) \geq E_{q_\phi(z|x)} [\log p_\theta(x|z)] - D_{\text{KL}}(q_\phi(z|x) ,|, q(z)) \]
这就是 ELBO(Evidence Lower BOund)公式(取下边界最大值)!
损失函数记作(取负号,损失函数求最小值):
\[ L_{\text{VAE}} = - E_{q_\phi(z|x)}[\log p_\theta(x|z)] + D_{\text{KL}}(q_\phi(z|x) ,|, q(z)) \]
第二项是让潜变量 \(q_\phi(z|x)\) 尽量拟合先验 \(q(z)\)(一般是标准正态)。
对于两个分布式高斯分布,KL 散度可以采用公式进行计算。有以下公式:
设两个 \(d\)-维正态分布:
- \( p = \mathcal{N}(\mu_p, \Sigma_p) \)
- \( q = \mathcal{N}(\mu_q, \Sigma_q) \) 有以下公式: \[ D_{\text{KL}}(p | q) = \frac{1}{2} \left[ \log \frac{|\Sigma_q|}{|\Sigma_p|} - d + \text{tr}(\Sigma_q^{-1} \Sigma_p) + (\mu_q - \mu_p)^T \Sigma_q^{-1} (\mu_q - \mu_p) \right] \]
因此,对于 VAE 损失函数中的 KL 散度 \[ D_{\text{KL}}(q_\phi(z|x) | q(z)) = \frac{1}{2} \sum_{i=1}^d \left( \mu_i^2 + \sigma_i^2 - \log \sigma_i^2 - 1 \right) \]
第一项的约束是为了让 \(z \to x\) 的重建尽可能好; 其中,求期望可以采用蒙特卡洛方法(收集训练数据集,就是对 x 进行采用),对所有样本求平均,就是最后的期望值,关键是每个特定图片的 \( \log p_\theta(x|z) \) 是什么?
给定的 \(x\) 可以得到 \(z\) 的分布,也就是 \(q_\phi(z|x)\),注意这里好像和第二项冲突,第二项指出 \(q_\phi(z|x)\) 越接近标准正态分布越好,但是通过某个确定的 \(x\) 得到的 \(z\) 好像不是标准正态分布?
VAE 的核心其实就是平衡这两者,第一项鼓励 \(q_\phi(z|x)\) 尽可能提供丰富、具体的信息,让 Decoder 可以重建出原始的 \(x\),第二项估计 \(q_\phi(z|x)\) 尽量接近正态分布。整体上,每个 \(x\) 对应一个「小偏离」的高斯,而训练目标是让所有这些偏离加起来,总体仍然接近标准正态,有些图片很卡通,有些不那么卡通,有些介于两者之间,符合标准正态分布,我们训练时候的目标就是能够找到这种卡通的维度,能够让 推断 Decoding 时,是在标准正态分布的维度上进行采样.
再根据特定的 \(x\) 约束后的 \(q_\phi(z|x)\) 进行采样(可以多次采样),并得到 \(z\),多次采样后的\(z\) 驱动 Decoding 得到的 多个 \(\hat{x}\),而这个多个 \(\hat{x}\) 确定的分布就是\( p_\theta(x|z) \)(其实条件分布 = 带噪声的随机变量变换,这里假设条件分布是Dirac分布,随机性由输入的随机变量决定),我们只需要让 \(\hat{x}\) 尽可能接近就行。
我们假设每个像素点的值符合高斯分布,且各个像素点相互独立,可以得到, \[ p_\theta(x|z) = \prod_{i=1}^D \mathcal{N}(x_i \mid \hat{x}_i, \sigma^2) \]
- 每个像素是高斯分布,均值为 \(\hat{x}_i\),方差为 \(\sigma^2\)。
- 最大化对数似然(MLE)就直接等价于最小化MSE: \[ \mathrm{MSE} = \sum_{i=1}^D (x_i - \hat{x}_i)^2 \]
def vae_loss(x, x_hat, mu, logvar):
# 注意求和,是指所有像素点的损失加起来
R_L = nn.functional.mse_loss(x_hat, x, reduction='sum')
# R_L = nn.functional.binary_cross_entropy(x_hat, x, reduction='sum')
D_KL = - 0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
# 总损失 = 重建误差 + KL 散度
return R_L + D_KL
也可以对标准化之后的像素点的值做伯努利分布的假设(像素要么是 1, 要是0),采用交叉熵作为损失函数(Binary Cross Entropy)。
\[ p_\theta(x|z) = \prod_{i=1}^D \mathrm{Bernoulli}(x_i \mid \hat{x}_i) \]
- 输出 \(\hat{x}_i\) 通过sigmoid,解释为「像素为1」的概率。
- 最终重构损失变成: \[ \mathrm{BCE} = - \sum_{i=1}^D \left[x_i \log \hat{x}_i + (1 - x_i) \log (1 - \hat{x}_i)\right] \]
最后的概率同样可以解释为灰度值。
如果我们要约束 \(z\) 的生成怎么做? 比如给一句话( \(y\) ),然后生成一张有确定方向的图片。
我们需要通过 \(y\) 生成 \(z\),而这个 \(z\),应该和 \(y\) 标记的图片生成的z具有相似的分布。 \[ q_y(z|x) ~ q_x(z|x) \]
这就是条件变分自编码器的核心思想。
\[ L_{\text{VAE}} = - E_{q_\phi(z|x)}[\log p_\theta(x|z)] + D_{\text{KL}}(q_\phi(z|x) ,|, q(z|y)) \]
层次变分自编码器(Hierarchical Variational Autoencoder)
和神经网络的多层结构化一样,VAE自然也会走向深度化。就变成了 层次变分自编码器 (HVAE)
高层编码全局结构,低层捕捉细节,有利于控制生成样本的特性。
HVAE 引入多层潜变量,假设潜变量分成 \( L \) 层,记为:
\[ z = { z_1, z_2, \dots, z_L } \]
对于编码器,其先验分布结构(自顶向下): \[ q(z) = q(z_L) \prod_{l=1}^{L-1} q(z_l | z_{l+1}) \]
后验分布结构(自底向上): \[ q(z | x) = q(z_1 | x) \prod_{l=2}^L q(z_l | z_{l-1}) \]
生成模型(解码器): \[ p(x | z_1) \]
即:
- 高层潜变量 \( z_L \) 捕捉抽象、全局的信息。
- 低层潜变量 \( z_1 \) 捕捉细节、局部的信息。
在训练时,HVAE 的目标函数是多层潜变量下的 ELBO:
\[ \log p(x) \geq E_{q(z|x)}\left[\log p(x|z_1)\right] - D_{\mathrm{KL}}(q(z|x) | q(z)) \]
具体展开为:
\[ \begin{aligned} L_{\mathrm{HVAE}}(x) = & \ E_{q(z_1 | x)}[\log p(x | z_1)] - \sum_{l=1}^L \left[ D_{\mathrm{KL}}(q(z_l | z_{l-1}) | q(z_l | z_{l+1})) \right] \end{aligned} \]
其中,\( z_0 = x \),方便公式统一表示,注意 HAVE 的损失函数 有多个 KL 散度相加,中间的层的 KL 散度类似条件变分自编码器。
扩散模式
Jarzynski 等式
\[ \int \rho(W, t_s) e^{-\beta W} dW = \frac{P_{final}}{P_{initial}} \]
MCP
MCP(模型上下文协议,Model Context Protocol)是由 Anthropic 于 2024 年 11 月推出的开放标准,旨在统一大型语言模型(LLM)与外部数据源和工具之间的通信协议。
说人话,这是提供了大模型工具的一个远程调用协议。在我们实现 function calling 的时候,会把 function 的信息以一种固定的文本格式内嵌到提示词里面,和问题打包一起传给大模型。从工程化的角度来看,有几个问题要解决。
- 每次增加
function的时候,不要改整个agent逻辑,这里可以用python的装饰器,把函数的注释信息自动抽取处理(函数名、详细描述、参数类型、参数含义、是否必须等等),存在一个全局变量中TOOLS,在生成提示词的时候,根据TOOLS去动态生成,这样 增加function就很容易了。 TOOLS以怎样的格式,嵌入到提示词中,大模型对工具(什么时候该调用)和对应的参数识别会更加准确率(React)?
function calling 是在一个程序包中实现的(TOOLS 作为一个全局变量),MCP 的出现,通过 http API,帮我们进一步解耦 function 的开发 和 agent 开发。 也就是后台用 python 开发的工具,可以用 js 调用。那么MCP 的服务器端,应该会提供 工具的描述信息(函数名、详细描述、参数类型、参数含义、是否必须等等)。 MCP的客户端,应该有一种约束,能够很方便的把工具的信息注入到提示词中,同时把工具的结果以一种通用的方式再次注入到提示词中,再次注入到提示词,根据大模型返回最后的回答。
架构
- 客户端程序,捕获用户问题(string),调用LLM(应该需要描述有哪些MCP server、本地的工具),LLM 会根据用户的问题,判断是否需要调用工具,并分析出工具。
- 远超调用MCP server,获取结果;
- 把结果放到提示词里面,在给到大模型
- 大模型返回最后的回答。
注意
- 客户端为什么知道MCP是多少的,有哪些工具,在第一次调用LLM前,应该先调用 MCP server,获取了工具的种类。
- 关键是 MCP的信息,如何注入到提示词中,以及MCP返回的信息,如何注入到提示词中?
- 还有MCP提供的协议具体规定了 json 的哪些内容?
大气状态预测
要对大气状态进行预报,我们需要构建模拟器:
\[ \Phi: (X^{t-\Delta t}, X^{t}) \to \hat{X}^{t+\Delta t}; \quad X^{t} \in R^{(V_s + V_a \times C) \times H \times W} \]
其中 \(X\) 表示大气状态变量(温度、气压等),\(t\) 表示当前事件,\(\Delta t\) 表示离散时间间隔, \(V_s\) 表示地表变量数(包括静态变量:地形,海陆,土壤),\(V_a\) 表示气压场变量数, \(C\) 表示气压层, \(H\) 表示维向网格数, \(W\) 表示经向网格数。
为了预报更长时间,用预报的数据作为输入,进行迭代计算
\[ \hat{X}^{t+k\times \Delta t} = \Phi(\hat{X}^{t+(k-2) \times \Delta t}, \hat{X}^{t+(k-1) \times \Delta t} ) \]
模式架构
相比于文本数据,在多样化的气象数据集上训练大型模型是一项更具挑战性的任务,因为气象数据的异质性更强。语言数据通常是同质的,而气象数据集则包含不同的变量、气压层次以及分辨率。此外,由于存储完整模拟输出的成本较高,许多数据来源仅通过在上述一个或多个维度上减少数据集大小的方式,提供部分数据子集。为了适应这种异质性的数据集,我们设计了一个灵活的编码器,将具有不同结构的数据集映射为标准化的三维张量,以便输入到模型的主干网络中。
ViTs
ViTs 是 Vision Transformers 的缩写,它是将 Transformer 架构 应用于 计算机视觉任务(如图像分类、目标检测、语义分割等)的一类模型。
将图片切割为 patch ,一张图片可能有10个 patch, 然后把每个 patch 类比成一个token,这样就能用 Transformer 去 抓取 patch 之间的空间关系。
patch 分割多大? 越多的patch,计算时间越长(全局 自注意力)。
Swin Transformer
Swin Transformer(Shifted Window Transformer)是 Vision Transformer 的一种改进版本。
相较于原始 ViT(对整幅图像进行全局注意力),Swin Transformer 引入了 局部窗口注意力 和 滑动窗口机制,以更好地兼顾计算效率和建模能力。
U-Net
通过卷积,把空间相关的信息,抽取到一个向量中(隐变量维度增加),通过池化,降低空间维度。迭代上述过程,也就是 U-Net 的 encode部分。在 decode 部分通过上采样,扩张空间维度,然后和 decode 中 卷积的输出部分合并到一起,在通过 decode中的卷积,将 隐变量 的信息还原到空间层面,迭代上述过程。
前端开发
CSS + tailwindcss
react
react-router
Redux + Redux Toolkit + Zustand
数据库
数据库
数据库是一堆有关联的数据集,如何描述关联?
数据模型
数据模型定义数据关系的范式。是数据结构的结构,比如
- 关系模型(Relational Model)
- 层次模型(Hierarchical Model)
- ...
关系模型
D 为域(集合),对于 一组域 \( \{ D_i | i = 1, 2, 3 ... \} \),设 \(a_i \in D_i\),称 \( < a_1, a_i, ..., a_n > \) 为定义在这组域上的元组。
这里的域,更准确率的数学描述应该是集合,一组域 => 集合的一个集合。
关系是指 一组域 \( \{ D_i | i = 1, 2, 3 ... \} \)的笛卡尔积(组合中的笛卡尔积计数)构成的全部元组集合 \( \{ < a_1, a_i, ..., a_n > | a_i \in D_i \} \) 中符合某种意义的元组子集合。
关系是一种集合!
元组 \( < a_1, a_i, ..., a_n > \) 是关系 \(R\) 的成员。
关系 \(R\) 中所有元组某个维度构成的域 \( A_i = \{ a_i | a_i \in D_i \} \) ,为关系 \(R\)的 某个属性。
属性 \(A_i\) 是一种域(集合)!是域 \(D_i\) 的子域
模式(关系模式) 是关系的实例化后的实体,实例化是指给定每个 \(A_i\) 的具体定义以及关系名称。
定义在关系模型上最重要的操作是关系代数和元组演算。
关系代数
关系代数的运算 是定义在元组集合上的,是从集合到集合的映射(存在一元和二元运算)。
基本关系代数运算
基本关系代数运算是指无法通过其它运算推导出来的基本运算。
1. 并(Union)
关系代数中的并,就是集合的并运算。 \[ R \cup S \]
条件:\(R\) 和 \(S\) 必须是同构关系(即属性个数和所属域一致)
2. 差(Difference)
差运算后的集合表示属于 $R$ 但不属于 $S$ 的元组集合。 \[R - S \]
条件:\(R\) 和 \(S\) 必须是同构关系(即属性个数和所属域一致)
3. 选择(Selection) \[ \sigma_{\theta}(R) \] 通过条件 \(\theta\),过滤集合 \(R\), 条件 \(\theta\) 为元组属性的比较运算 + 布尔运算,例如:
\[\sigma_{price > 30}(Product)\]
4. 投影(Projection) \[ \pi_{A_1, A_2, \dots, A_k}(R) \]
表示从关系 \(R\) 中选取属性 \(A_1, A_2, \dots, A_k\)。 类似向量空间中的降维,从高纬度投影到低维度。
5. 笛卡尔积(Cartesian Product)
\[ R \times S \]
笛卡尔积得到的是 \(R\) 与 \(S\) 元组的所有可能组合,结果元组数为 \((r, s)\)。
扩展代数关系运算
扩展代数运算可以有基本代数运算组合得到,定义扩张运算可以更加方便地写出表达式
1. 交 (INTERSECT)
关系代数中的交,就是集合的交运算
\[ R \cap S = R - ( R - S )\]
条件:\(R\) 和 \(S\) 必须是同构关系(即属性个数和所属域一致)
2. 连接(Join)
θ-连接(Theta Join) \[R \bowtie_{\theta} S = \sigma_{\theta}(R \times S)\]
相等连接 \[R \bowtie_{e} S = \sigma_{e}(R \times S)\] 相等连接是特殊的 θ-连接,条件 \(\theta\) 只能是等于表达式。
自然连接(Natural Join) \[R \bowtie S\] 自动在相同属性名上进行匹配,连接后同名属性消失。
3. 除法(Division)
\[R \div S = \{ a \mid \forall b \in S, (a, b) \in R \}\]
表示那些与 \(S\) 中的所有 \(b\) 组合都在 \(R\) 中的 \(a\)。
\[ R \div S = \pi_X(R) - \pi_X ( ( \pi_X(R) \times S ) - R) \]
举个例子,所有选修了 S 中所有课程的学生。
\[R(Student, Course)\] \[S(Course)\]
\[ R \div S = \pi_{Student}(R) - \pi_{Student} ( ( \pi_{Student}(R) \times S ) - R) \]
元组演算
元组演算基于逻辑谓词,并使用元组变量来表达查询条件(集合的定义形式)。
查询结果是所有满足条件 \( P(t) \) 的 \( t \) 所组成的集合. \[\{ t | P(t) \}\]
- \( t \) 是元组
- \( P(t) \) 是逻辑表达式,表示元组 \( t \) 应满足的条件
\( P(t) \) 的递归定义可以写作
P(t) ::=
t.A θ c // 属性与常量比较: 原子谓词
| t1.A θ t2.B // 两个元组的属性比较: 原子谓词
| t ∈ R // t 属于关系 R: 原子谓词
| ¬P(t) // 逻辑非
| P(t) ∧ Q(t) // 逻辑与
| P(t) ∨ Q(t) // 逻辑或
| ∃ s (P(s)) // 存在某个元组 s 满足
| ∀ s (P(s)) // 所有元组 s 满足
| P(t) → Q(t) // 可选扩展项 ¬P(t) ∨ Q(t)
| ∃ (s ∈ R) (P(s)) // 可选扩展项 ∃ s (s ∈ R ∧ P(s))
| ∀ (s ∈ R) (P(s)) // 可选扩展项 ∀ s (s ∈ R → P(s))
其中
- \( P(t) \) 和 \( Q(t) \) 都是逻辑表达式。
- 元组 \( t \) 的属性 \( A\) 的值表示为 \( t.A \)
- \( \exists \) 为 存在(存在量词)
- \( \forall \) 为 所有(全称量词)
举个例子,找出选修了所有 张三 任教课程的学生, 案例数据库的所有关系模式如下:
Student(sid, sname)
Course(cid, cname, teacher)
Enroll(sid, cid)
采用最基础的语法书写 \[ \{s | s \in Student \land \forall c (\lnot (c \in Course \land c.teacher = "张三") \lor (\exists e (e \in Enroll \land e.sid = s.sid \land e.cid = c.cid) ) ) \} \] 对每门课程我们检查:
- 如果它不是张三的课,跳过(条件自然为真)
- 如果它是张三的课,必须存在一条选课记录,说明学生选了它
加上蕴含扩展 \[ \{s | s \in Student \land \forall c (c \in Course \land c.teacher = "张三" \rightarrow (\exists e (e \in Enroll \land e.sid = s.sid \land e.cid = c.cid) ) ) \} \]
对每门课程我们检查:
- 如果它不是张三的课,跳过
- 如果它是张三的课,必须存在一条选课记录,说明学生选了它
量词扩展定义域写法。 \[ \{ s | s \in Student \land \forall c \in \{c | c \in Course \land c.teacher = "张三" \} (\exists e \in Enroll (e.sid = s.sid \land e.cid = c.cid) ) \} \]
对每门张三的课程我们检查:
- 必须存在一条选课记录,说明学生选了它
用关系代数来写查询 \[ Student \Join (\pi_{sid, cid}(Student \Join Enroll) \div \pi_{cid}(\sigma_{teacher="张三"}(Course))) \]
约束条件
候选码:每个元组都不一样最小属性集(唯一性,最小性)
可以选取一个候选码作为主键(Primary Key)。 外键是一种关系的特殊属性,该属性是其他关系的主键。
- 约束条件1: 主键属性不能为未定义
- 约束条件2: 外键的属性必须满足外键的已取值范围(不是定义域的范围)
- 约束条件3: 属性定义域的约束条件
数据库管理系统
数据库管理系统一种软件实现(比如 mysql), 用来管理 多个 基于某种 数据模型的数据库的软件。
关系数据库管理系统
基于关系模型的 数据库管理系统实现(比如 Postgres )。
在用户层面希望看到的功能。
- 用户信息的增删改查(权限管理)
- 数据库的增删改查(多张表,依靠外键关联?)
- 关系/表的增删改查( schema/模式 )
- 数据的增删改查(view/data: 行/元组)
增删改查的ACID特性:原子性、一致性、隔离性、持久性
在关系数据库管理系统实现的关系数据结构叫做表。 表可以看作是关系的一种表达形式(从集合 到 规则的长方形表格)。
索引
索引是关系数据库中对某一列或多个列的值进行预排序的数据结构, 为了加速查询操作而创建的数据结构。
主键是一种特殊的索引。
视图
视图(View)是关系型数据库中的一种虚拟表,它本身不存储数据,而是对一个或多个真实表(或其他视图)的查询结果进行封装。
可以屏蔽掉 真实表 的细节(为用户提供一致的表结构,真实表改了,视图可以不变)。
SQL
SQL(Structured Query Language,结构化查询语言)是一种用于管理关系型数据库的标准语言。
SQL 是一种声明式语言,是构建在元组演算和关系代数之上的。
SQL 可以分为 数据操作语言(DML, Data Manipulation Language)、 数据定义语言(DDL, Data Definition Language) 和 数据控制语言(DCL, Data Control Language)
数据控制语言
用户的增删改查
增加
CREATE USER username WITH PASSWORD 'password';
CREATE ROLE xiaolh WITH LOGIN PASSWORD 'xiaolh123456'; -- 或更常用:
删除
DROP USER username;
DROP ROLE username;
修改
ALTER USER username WITH PASSWORD 'newpassword';
ALTER USER username RENAME TO new_username;
ALTER USER username WITH SUPERUSER; -- 赋予超级权限
ALTER USER username WITH NOSUPERUSER; -- 撤销超级权限
权限管理
-- 增加
GRANT SELECT, INSERT ON tbname TO username;
GRANT ALL PRIVILEGES ON DATABASE dbname TO username;
ALTER USER xiaolh WITH CREATEDB; -- 创建库的权限
ALTER USER xiaolh WITH NOCREATEDB;
-- 回收
REVOKE SELECT ON tbname FROM username;
REVOKE ALL PRIVILEGES ON DATABASE dbname FROM username; -- 给表的所有权限
常见权限有SELECT , INSERT, UPDATE, DELETE, ``ALL PRIVILEGES `。
查看
\du -- 查看用户及权限
SELECT * FROM pg_roles;
数据定义语言
数据库的增删改查
增加
CREATE DATABASE dbname;
删除
DROP DATABASE dbname;
修改
ALTER DATABASE dbname RENAME TO new_dbname;
ALTER DATABASE dbname OWNER TO new_owner; -- 给其他用户
查看
\l -- 查看所有数据库(在 psql 中)
SELECT datname FROM pg_database; -- SQL 查询数据库名
数据表的增删改查
增加
CREATE TABLE tbname (
列名1 数据类型 [约束],
列名2 数据类型 [约束],
...
);
常见约束有PRIMARY KEY , UNIQUE, NOT NULL, CHECK, FOREIGN KEY,
CREATE TABLE score (
student_id INT,
course_id INT,
score FLOAT CHECK (score >= 0 AND score <= 100),
FOREIGN KEY (student_id) REFERENCES student(id)
);
删除
DROP TABLE tbname;
TRUNCATE TABLE tbname; -- 清空表中所有数据,但保留表结构
修改
ALTER TABLE tbname RENAME TO new_name; -- 修改表格名称
ALTER TABLE tbname ADD COLUMN age INT; -- 添加字段
ALTER TABLE tbname DROP COLUMN age; -- 删除字段
ALTER TABLE tbname RENAME COLUMN username TO new_name; -- 修改字段名称
ALTER TABLE tbname ALTER COLUMN username TYPE VARCHAR(100); -- 修改字段类型
索引
CREATE INDEX idx_name ON tbname(username);
DROP INDEX idx_name;
主键/外键
ALTER TABLE tbname ADD CONSTRAINT 约束名 PRIMARY KEY(id);
ALTER TABLE tbname ADD CONSTRAINT 约束名 FOREIGN KEY(office_id) REFERENCES office(id);
查看
\di -- psql 命令 查询索引
\dt -- psql 命令 查看当前数据库所有表
\d tbname -- psql 命令 查看表结构
\z tbname -- psql 命令 查看表权限
数据操作语言
主要命令:
- INSERT:向表中插入数据。
- DELETE:删除表中的数据。
- UPDATE:更新表中的数据。
- SELECT:从一个或多个表中检索数据。
向表中插入数据
语法
INSERT INTO table_name (column1, column2) VALUES (value1, value2);
INSERT INTO students (class_id, name, gender, score) VALUES
(2, 'name1', 'M', 80),
(2, 'name2', 'M', 81);
删除表中的数据
语法
DELETE FROM table_name WHERE condition;
DELETE FROM students WHERE id=1;
更新表中的数据
语法
UPDATE table_name SET column1 = value1 WHERE condition;
检索库中的数据
语法
SELECT [DISTINCT] 列表达式
FROM 表或子查询
[JOIN 子句]
[WHERE 条件]
[GROUP BY 分组列 [HAVING 条件]]
[ORDER BY 排序列 [ASC|DESC]]
[LIMIT 限制行数 [OFFSET起始行]]
注意事项
- 字符的 WHERE 条件,可以使用通配符进行模糊查询,LIKE(模糊查询) 和 _,%(通配符)
- JOIN 子句,分为 [INNER/LEFT/RIGHT/FULL] JOIN(自连接,内连接,外连接:处理null)
- HAVING 条件 是针对 GROUP BY 后的集合
- 列表达式是指 元组属性的算数表达式 + 聚合函数(MIN、MAX、AVG、SUM等),元组属性本身也是列表达式
- AS 赋值语句,可以把表达式的值进行赋值,或者重命名属性/表名称
- FROM 中的子查询 可以看作一种临时的视图(本应该为表名的地方,变为一个动态的匿名表)
- WHERE 中子查询有三种,包括 IN, \(\theta - all/some\) 和 EXISTS
- 基于集合操作,UNION, INTERSECT, EXCEPT
其他扩展语法
- CASE WHEN 逻辑判断(等价于 if-else)
简单案例
SELECT Title FROM movies
where Director = "John Lasseter"
order by year Desc
limit 1 offset 3
一些简单的子查询案例
选出所在院系在北京的学生。
SELECT name
FROM Student
WHERE deptID IN (
SELECT deptID
FROM Department
WHERE location = 'Beijing'
);
元组演算表示: \[ \{ s.name \mid s \in Student \land \exists \ deptID \in \{ d.deptID \mid d \in Department \land d.location = 'Beijing' \} \ (s.deptID = deptID) \} \]
选出比 3 号院系所有学生分数都高的学生。
SELECT name
FROM Student
WHERE score > ALL (
SELECT score
FROM Student
WHERE deptID = 3
);
元组演算表示:
\[ \{ s.name \mid s \in Student \land \forall score \in \{ t.score \mid t \in Student \land t.deptID = 3 \} \ (s.core > score) \} \]
注意 \(\theta - all/some \) 子句 与 元组演算的定义域扩展语法 有着很好的对于关系。
选出分数小于 3 号院系某些学生的学生。
SELECT name
FROM Student
WHERE score < SOME (
SELECT score
FROM Student
WHERE deptID = 3
);
元组演算表示: \[ \{ s.name \mid s \in Student \land \exists \ score \in \{ t.score \mid t \in Student \land t.deptID == 3 \} \ (s.score < score) \} \]
关于关系代数的案例
交
SELECT name FROM Student
INTERSECT
SELECT name FROM Course;
并
SELECT name FROM Student
UNION
SELECT name FROM Course;
postgresql
PostgreSQL is a powerful, open source object-relational database system with over 35 years of active development that has earned it a strong reputation for reliability, feature robustness, and performance.
安装
下载
wget https://ftp.postgresql.org/pub/source/v17.4/postgresql-17.4.tar.gz
启动
初始化一个目录为数据库目录
initdb -D /public/home/bedrock/envs/database
开始数据库服务
pg_ctl -D /public/home/bedrock/envs/database -l logfile start
[bedrock@node1 database]$ netstat -nplt | grep postgres
(Not all processes could be identified, non-owned process info
will not be shown, you would have to be root to see it all.)
tcp 0 0 127.0.0.1:5432 0.0.0.0:* LISTEN 14276/postgres
tcp6 0 0 ::1:5432 :::* LISTEN 14276/postgres
命令行连接数据库
psql -U bedrock -h localhost -d postgres
远程连接
host all all 0.0.0.0/0 md5 # pg_hba.conf
host all all ::/0 md5 # pg_hba.conf
listen_addresses = '*' # postgresql.conf
pg_ctl -D /public/home/bedrock/envs/database -l logfile restart
用法
import psycopg2
serverKargs = dict( # 连接参数
host = 'localhost',
port = '5432',
user = 'xiaolh',
password = 'xiaolh123456',
database = 'obs',
)
with psycopg2.connect(**serverKargs) as fh:
with fh.cursor() as cursor:
cursor.execute("SELECT version();")
print("PostgreSQL info:", cursor.fetchone())
# 插入
data = [("demo1", "demo1@expm.com"), ("demo2", "demo2@expm.com"), ("demo3", "demo3@expm.com")]
cursor.executemany("INSERT INTO users (name, email) VALUES (%s, %s)", data)
fh.commit() # 提交更改
# 删除
cursor.execute("DELETE FROM users WHERE name = %s", ("demo3",))
fh.commit() # 提交更改
# 更新
oldName, newName = "demo1", "xiaolh1"
cursor.execute("UPDATE users SET name = %s WHERE name = %s", (newName, oldName))
fh.commit() # 提交更改
# 查看
cursor.execute("SELECT * FROM users LIMIT 15")
for row in cursor.fetchall():
print(row)
支持的数据结构
PostgreSQL支持的数据结构非常丰富,官网文档给了详细说明。
入门时可能会用到的数据据结构:
- 数字相关:
- 整数类型(integer types):
- smallint,2字节
- integer,4字节
- bigint,8字节
- 序列类型(serial types): 序列类型通常用于自增ID,一般是为了PRIMARY KEY。
- smallserial,2字节
- serial,4字节
- bigserial,8字节
- 浮点
- float4,单精度,4字节
- float8,双精度,8字节
- 整数类型(integer types):
- 字符类型
- varchar(n), 有长度限制的字符串
- char(n),定长字符串,长度不足则向后填充空白字符
- text,不限长度
- 时间
- timestamp,'2019-12-12 11:30:30'
- JSON 类型
- json
- jsonb
数据建模
在实际开发中,设计数据库是有一些规律和方法可循的,其中比较常见、也比较有名的一种方法就是使用 ER 模型(实体-关系模型)。
从需求描述到最终写出 SQL 代码,其实就是一个不断消除模糊、逐步明确细节的过程。而 ER 模型提供了一种清晰的思考框架,它引导我们从实体和关系这两个角度出发,去理清需求中涉及的对象和它们之间的联系,从而让原本不清楚的地方变得明确起来。
实体(Entity)表示一个独立、具体的对象。我们可以粗略地把实体理解为名词,比如“计算机”、“雇员”、“歌曲”或“数学定理”。
关系(Relationship)用来描述两个或多个实体之间是如何关联的。可以粗略地把关系看作是动词,比如“拥有”、“雇佣”、“演唱”或“引用”。
如何确定需要哪些实体、哪些是关系,其实是一门艺术。选择恰当的实体和关系,不仅能帮助我们更深入地理解需求,还能设计出结构更清晰、效率更高的数据库表。
这么说很抽象,我们以一个假想的项目,来走通从需求到观念模型,再到数据模型。
视频知识付费平台 (MindTrail)
需要满足的需求
- 平台支持用户的注册和管理。
- 不同用户有不同的角色(学生、老师、管理员、审核员)和权限。
- 教师发布课程视频,学生购买课程(打包视频),也可以购买某个视频,课程视频不能高于所有时评的价格总和。
- 一个课程有多个视频,学生购买后,需要记录学习进度。
- 审核员审核教师发布的视频。
- 管理员有权对用户、课程、视频进行管理(增删改查)。
对象有
- 角色,属性有: 角色ID,名称,权限级别。
- 用户,属性有: 用户ID,名称,性别,自我介绍,邮件,电话,出生年月,角色ID,创建时间
- 学科,属性有: 学科ID,名称,学科介绍
- 课程,属性有: 课程ID,名称,学科ID,课程简介,价格,状态(新建、发布、删除),创建时间
- 视频,属性有: 视频ID,名称,学科ID,视频简介,章节,状态(完成上传、提交审核、完成审核、完成发布、删除),价格,课程ID,上传时间
- 产品,属性有:产品ID,产品类型(视频、或者课程),课程ID,视频ID,价格
关系
- 视频归档到课程,老师可以把视频打包到某个课程(多对多的关系)。属性:归档ID,视频ID,课程ID
- 学生购买产品ID,属性:账单ID,用户ID,产品ID,价格,状态(创建,完成付款),付款时间。
- 审核员审核视频,属性:审核单ID,用户ID,视频ID,状态(待审核,完成审核)
- 学生学习课程,属性:学习ID,用户ID,产品ID,状态(未开始,学习中,完成),进度(第几个视频的什么位置)
E-R图如下
erDiagram
roles {
int role_id
varchar name
int permission_level
}
users {
int user_id
varchar name
enum gender
text bio
varchar email
varchar phone
date birthdate
int role_id
datetime created_at
}
subjects {
int subject_id
varchar name
text description
}
courses {
int course_id
varchar name
int subject_id
text description
decimal price
enum status
datetime created_at
}
videos {
int video_id
varchar name
int subject_id
text description
varchar chapter
enum status
decimal price
int teacher_id
datetime uploaded_at
}
video_course_archive {
int archive_id
int video_id
int course_id
}
products {
int product_id
enum product_type
int video_id
int course_id
decimal price
}
purchases {
int purchase_id
int user_id
int product_id
decimal price
enum status
datetime paid_at
}
audits {
int audit_id
int user_id
int video_id
enum status
datetime audited_at
}
study_progress {
int progress_id
int user_id
int product_id
enum status
varchar progress_detail
datetime updated_at
}
%% 关系
users }o--|| roles : "has role"
users ||--o{ purchases : "makes"
users ||--o{ audits : "reviews"
users ||--o{ study_progress : "studies"
users ||--o{ videos : "uploads"
subjects ||--o{ courses : "includes"
subjects ||--o{ videos : "includes"
videos ||--o{ video_course_archive : "linked to"
courses ||--o{ video_course_archive : "linked to"
videos ||--o{ products : "can be product"
courses ||--o{ products : "can be product"
products ||--o{ purchases : "is purchased"
products ||--o{ study_progress : "is studied"
videos ||--o{ audits : "are reviewed"
创建表格和数据
-- 建立数据库
-- CREATE DATABASE mindtrail;
-- =============== 枚举类型定义 ===============
-- 性别类型
CREATE TYPE gender_enum AS ENUM ('男', '女');
-- 视频状态
CREATE TYPE video_status_enum AS ENUM (
'完成上传', '提交审核', '完成审核', '完成发布', '删除'
);
-- 课程状态
CREATE TYPE course_status_enum AS ENUM (
'新建', '发布', '删除'
);
-- 产品类型
CREATE TYPE product_type_enum AS ENUM (
'视频', '课程'
);
-- 购买状态
CREATE TYPE purchase_status_enum AS ENUM (
'创建订单', '完成付款'
);
-- 审核状态
CREATE TYPE audit_status_enum AS ENUM (
'待审核', '完成审核'
);
-- 学习状态
CREATE TYPE study_status_enum AS ENUM (
'未开始', '学习中', '完成'
);
-- =============== 主体表 ===============
-- 角色
CREATE TABLE roles (
role_id SERIAL PRIMARY KEY,
name VARCHAR(50) NOT NULL,
permission_level INT NOT NULL
);
-- 用户
CREATE TABLE users (
user_id SERIAL PRIMARY KEY,
name VARCHAR(100) NOT NULL,
gender gender_enum,
bio TEXT,
email VARCHAR(100),
phone VARCHAR(20),
birthdate DATE,
role_id INT REFERENCES roles(role_id),
created_at TIMESTAMP DEFAULT CURRENT_TIMESTAMP
);
-- 学科
CREATE TABLE subjects (
subject_id SERIAL PRIMARY KEY,
name VARCHAR(100) NOT NULL,
description TEXT
);
-- 课程
CREATE TABLE courses (
course_id SERIAL PRIMARY KEY,
name VARCHAR(200) NOT NULL,
subject_id INT REFERENCES subjects(subject_id),
description TEXT,
price NUMERIC(10,2) NOT NULL DEFAULT 0,
status course_status_enum DEFAULT '新建',
created_at TIMESTAMP DEFAULT CURRENT_TIMESTAMP
);
-- 视频
CREATE TABLE videos (
video_id SERIAL PRIMARY KEY,
name VARCHAR(200) NOT NULL,
subject_id INT REFERENCES subjects(subject_id),
description TEXT,
chapter VARCHAR(100),
status video_status_enum DEFAULT '完成上传',
price NUMERIC(10,2) NOT NULL DEFAULT 0,
course_id INT, -- 可选冗余字段,如果需要快速查询
teacher_id INT REFERENCES users(user_id),
uploaded_at TIMESTAMP DEFAULT CURRENT_TIMESTAMP
);
-- 产品(课程或视频)
CREATE TABLE products (
product_id SERIAL PRIMARY KEY,
product_type product_type_enum NOT NULL,
course_id INT REFERENCES courses(course_id),
video_id INT REFERENCES videos(video_id),
price NUMERIC(10,2) NOT NULL
);
-- =============== 关系表 ===============
-- 视频归档到课程(多对多)
CREATE TABLE video_course_archive (
archive_id SERIAL PRIMARY KEY,
video_id INT NOT NULL REFERENCES videos(video_id),
course_id INT NOT NULL REFERENCES courses(course_id)
);
-- 购买记录(产品)
CREATE TABLE purchases (
purchase_id SERIAL PRIMARY KEY,
user_id INT NOT NULL REFERENCES users(user_id),
product_id INT NOT NULL REFERENCES products(product_id),
price NUMERIC(10,2) NOT NULL,
status purchase_status_enum DEFAULT '创建',
paid_at TIMESTAMP
);
-- 视频审核
CREATE TABLE audits (
audit_id SERIAL PRIMARY KEY,
user_id INT NOT NULL REFERENCES users(user_id), -- 审核员
video_id INT NOT NULL REFERENCES videos(video_id),
status audit_status_enum DEFAULT '待审核',
audited_at TIMESTAMP DEFAULT CURRENT_TIMESTAMP
);
-- 学习进度
CREATE TABLE study_progress (
progress_id SERIAL PRIMARY KEY,
user_id INT NOT NULL REFERENCES users(user_id),
product_id INT NOT NULL REFERENCES products(product_id),
status study_status_enum DEFAULT '未开始',
progress_detail VARCHAR(200), -- 示例:视频3-00:14:52
updated_at TIMESTAMP DEFAULT CURRENT_TIMESTAMP
);
插入一些假数据
INSERT INTO roles (name, permission_level) VALUES
('学生', 1),
('老师', 2),
('审核员', 3),
('管理员', 4);
INSERT INTO users (name, gender, bio, email, phone, birthdate, role_id) VALUES
('张三', '男', '热爱学习', 'zhangsan@example.com', '13800000001', '2000-01-01', 1),
('李四', '女', '资深教师', 'lisi@example.com', '13800000002', '1990-02-15', 2),
('王五', '男', '审核员', 'wangwu@example.com', '13800000003', '1995-03-25', 3),
('赵六', '女', '管理员', 'zhaoliu@example.com', '13800000004', '1985-04-30', 4);
INSERT INTO subjects (name, description) VALUES
('数学', '关于数学的课程'),
('物理', '关于物理的课程'),
('编程', '学习编程的课程');
INSERT INTO courses (name, subject_id, description, price, status) VALUES
('高等数学', 1, '学习高等数学的基础课程', 199.99, '发布'),
('大学物理', 2, '物理学的基础课程', 159.99, '发布'),
('Python 编程入门', 3, 'Python 编程的入门课程', 129.99, '新建');
UPDATE courses SET user_id = 2;
INSERT INTO videos (name, subject_id, description, chapter, status, price, course_id, teacher_id) VALUES
('高等数学 - 第一章', 1, '高等数学第一章的基础讲解', '第一章', '完成上传', 49.99, 1, 2),
('高等数学 - 第二章', 1, '高等数学第二章讲解', '第二章', '提交审核', 49.99, 1, 2),
('大学物理 - 第一章', 2, '物理学第一章的基础讲解', '第一章', '完成审核', 59.99, 2, 2),
('Python 编程入门 - 第1节', 3, 'Python 编程的基础知识', '第1节', '完成上传', 39.99, 3, 2);
INSERT INTO products (product_type, course_id, video_id, price) VALUES
('课程', 1, NULL, 199.99),
('课程', 2, NULL, 159.99),
('视频', NULL, 1, 49.99),
('视频', NULL, 2, 49.99),
('视频', NULL, 3, 59.99),
('视频', NULL, 4, 39.99);
INSERT INTO purchases (user_id, product_id, price, status, paid_at) VALUES
(1, 1, 199.99, '完成付款', '2025-04-01 10:00:00'),
(2, 2, 159.99, '完成付款', '2025-04-02 11:00:00'),
(3, 3, 49.99, '创建订单', NULL),
(4, 4, 39.99, '完成付款', '2025-04-03 12:00:00');
INSERT INTO audits (user_id, video_id, status, audited_at) VALUES
(3, 2, '完成审核', '2025-04-02 14:00:00'),
(3, 3, '完成审核', '2025-04-03 15:00:00');
INSERT INTO study_progress (user_id, product_id, status, progress_detail, updated_at) VALUES
(1, 1, '学习中', '视频1-00:05:00', '2025-04-01 12:00:00'),
(2, 2, '未开始', NULL, '2025-04-02 13:00:00'),
(4, 4, '已完成', '视频4-01:30:00', '2025-04-03 13:00:00');
进行查询,所有学生及其购买的课程。
SELECT u.user_id, u.name AS student_name, c.name AS course_name, p.price AS course_price, pu.status AS purchase_status
FROM users u
JOIN purchases pu ON u.user_id = pu.user_id
JOIN products p ON pu.product_id = p.product_id
JOIN courses c ON p.course_id = c.course_id
WHERE u.role_id = 1;
大数据
当数据量达到海量(TB级别以上),并且还在持续增长,同时数据类型也变得多样化时,我们称之为大数据。 传统的数据库技术已经很难满足这些海量数据在存储和计算上的高效处理需求。
解决海量数据带来的挑战的技术,被称为大数据技术。
一个很自然的思路就是采用分布式架构,也就是将数据的计算和存储能力分散到多台机器上进行协同处理(这与传统的磁盘阵列方式不同)。目前,主流的大数据技术实现大多来自 Apache 软件基金会。
Apache Hadoop 是大数据技术的一种实现方式。Hadoop 是一个框架,允许使用简单的编程模型跨计算机集群对大型数据集进行分布式处理。最小 Hadoop 集群包含三个组件,分别为 作为分布式存储的 Hadoop 分布式文件系统 (HDFS)、用于调度和管理集群的 Hadoop YARN 以及作为执行引擎进行并行处理的 Hadoop MapReduce。
另一方面,Apache Spark 是另一种可选的数据处理执行引擎(更快)。关键区别在于,Spark 使用弹性分布式数据集 (RDD) 并将其存储在内存中,从而显著提升了性能,远超 MapReduce。Spark 可以独立运行并实现基本功能。然而,与 Hadoop 结合使用时,Spark 可以利用 Hadoop 的功能进行集群管理、容错、安全性等。
Hive 是一款分析工具,它利用存储在 HDFS 中的数据,并使用 Spark 或 MapReduce 作为执行引擎。这使得用户可以使用熟悉的 SQL 语句来分析数据,从而帮助开发人员更轻松地从数据中挖掘洞察。
在大数据的架构中,需要到把数据导入到 HDFS 系统中(为了存储大量数据),然后用 MapReduce 或者 Spark 对文件进行处理(对大量数据进行计算),或者用 Hive 等应用工具进行数据吹,形成新的文件,然后再把分析、统计凝练之后的数据导出 HDFS 系统(处理之后的数据会小很多,在HDFS中直接操作太慢了)。
在这个过程中,可能会涉及到 Flume 和 Sqoop 对非结构化数据和结构化数据进行导入导出。
因此整个流程涉及到 数据收集,数据处理,数据导出,这些任务之间有相互依赖关系, 可以用 Azkaban 进行任务流管理 (cron + 依赖管理)
搭建测试环境
了解系统内部(底层)的工作原理是非常重要的。 为了做到这一点,我们首先需要搭建一个成本低、灵活性高的开发环境。
在这种情况下,使用 Docker 来启动和管理大气数据生态系统中的各个组件,无疑是一个理想的选择。它不仅方便搭建环境、隔离依赖,还能帮助我们快速测试和理解各个模块的运行机制。
具体参考该仓。
hadoop
Apache Hadoop 是大数据技术的一种实现方式。Hadoop 是一个框架,允许使用简单的编程模型跨计算机集群对大型数据集进行分布式处理。最小 Hadoop 集群包含三个组件,分别为 作为分布式存储的 Hadoop 分布式文件系统 (HDFS)、用于调度和管理集群的 Hadoop YARN 以及作为执行引擎进行并行处理的 Hadoop MapReduce。
HDFS
HDFS 是一个文件系统,其命令行操作类似FTP。
命令行
| 操作分类 | 命令格式 | 示例 | 说明 |
|---|---|---|---|
| 目录操作 | hdfs dfs -ls /路径 | hdfs dfs -ls /user/hive | 查看 HDFS 路径下的文件 |
hdfs dfs -mkdir /路径 | hdfs dfs -mkdir /user/test | 创建 HDFS 目录 | |
hdfs dfs -mkdir -p /a/b/c | hdfs dfs -mkdir -p /data/input | 递归创建目录 | |
hdfs dfs -rm -r /路径 | hdfs dfs -rm -r /data/old | 递归删除目录或文件 | |
hdfs dfs -rmdir /路径 | hdfs dfs -rmdir /user/empty_dir | 删除空目录 | |
hdfs dfs -mv 源 目标 | hdfs dfs -mv /a.txt /backup/a.txt | 移动/重命名 | |
| 文件操作 | hdfs dfs -put 本地 HDFS | hdfs dfs -put a.csv /data/ | 上传文件到 HDFS |
hdfs dfs -get HDFS 本地 | hdfs dfs -get /data/b.txt ./ | 下载文件 | |
hdfs dfs -cat /文件 | hdfs dfs -cat /data/file.txt | 查看文件内容 | |
hdfs dfs -tail /文件 | hdfs dfs -tail /logs/job.log | 查看文件尾部 | |
hdfs dfs -text /文件 | hdfs dfs -text /data/file.orc | 查看 ORC 等二进制文件 | |
hdfs dfs -du -h /路径 | hdfs dfs -du -h /user/hive/warehouse | 查看文件/目录大小 | |
hdfs dfs -chmod 755 /路径 | hdfs dfs -chmod 755 /user/test | 修改权限 | |
hdfs dfs -chown 用户:组 /路径 | hdfs dfs -chown hive:hadoop /data/ | 修改属主 | |
| 空间统计 | hdfs dfs -df -h | hdfs dfs -df -h | 查看 HDFS 空间使用情况 |
| 其他 | hdfs dfsadmin -report | hdfs dfsadmin -report | 查看 HDFS 集群状态 |
HDFS 接口
HDFS 提供了一套 RESTful 风格的 HTTP 接口,称为 WebHDFS, 允许用户通过 HTTP 协议对 HDFS 中的数据进行操作,方便跨语言、跨平台集成调用。
# 创建空文件
PUT http://namenode:9870/webhdfs/v1/user/hadoop/test.txt?op=CREATE
# 上传文件 [Content-Type: application/octet-stream]
PUT http://<datanode>:9870/webhdfs/v1/user/hadoop/test.txt?op=CREATE&data=true
# 读取文件
GET http://namenode:9870/webhdfs/v1/user/hadoop/test.txt?op=OPEN
# 获取文件状态
GET http://namenode:9870/webhdfs/v1/user/hadoop/test.txt?op=GETFILESTATUS
MapReduce
Hadoop Streaming 是 Hadoop 提供的一个通用接口,允许用标准输入输出格式写 Mapper 和 Reducer。
用 python 实现 MapReduce,可以理解为 LINUX 的管道。
flowchart TD
A["HDFS 输入数据"] --> B["Mapper 脚本: map.py"]
B --> C["Shuffle & Sort (Hadoop 自动完成)"]
C --> D["Reducer 脚本: reduce.py"]
D --> E["HDFS 输出目录"]
可以在不启动 Hadoop 的情况下,使用sort进行测试
chmod +x map.py reduce.py
cat data.txt | python map.py | sort | python reduce.py
词频统计 map.py
#!/usr/bin/env python3
import sys
for line in sys.stdin:
for word in line.strip().split():
print(f"{word},1")
词频统计 reduce.py
#!/usr/bin/env python3
import sys
current_word = None
count = 0
for line in sys.stdin:
word, val = line.strip().split(',')
val = int(val)
if word == current_word:
count += val
else:
if current_word:
print(f"{current_word}, {count}")
current_word = word
count = val
if current_word:
print(f"{current_word}, {count}")
提交
yarn jar /opt/hadoop/share/hadoop/tools/lib/hadoop-streaming-*.jar \
-input /input/data.txt \
-output /output/wordcount \
-mapper map.py \
-reducer reduce.py \
-file map.py \
-file reduce.py
yarn
yarn 是一个任务调度器,类似 HPC 中的 slurm。 yarn 支持 Web UI,上手能能快一些。
查看集群状态的一些命令
yarn node -list
yarn clust --help
任务相关
yarn jar hadoop-mapreduce-examples-3.4.1.jar pi 10 15 # 提交一个任务
yarn application -list # 查看任务小黄太
yarn application -kill <ApplicationId> # 杀死任务
通过 yarn 提交 spark 应用
spark-submit \
--master yarn \
--deploy-mode cluster \
wordcount.py \
hdfs:///input.txt \
hdfs:///output/
spark
spark 对 python 的支持更好。
搭建试验环境
通过 Dcoker 安装 Spark,拉取bitnami/spark
docker pull bitnami/spark:latest
通过 docker-compose 配置集群,保存 spark/docker-compose.yml
services:
spark:
image: docker.io/bitnami/spark
environment:
- SPARK_MODE=master
- SPARK_RPC_AUTHENTICATION_ENABLED=no # 禁用了 RPC 认证、加密和 SSL,以简化配置
- SPARK_RPC_ENCRYPTION_ENABLED=no
- SPARK_LOCAL_STORAGE_ENCRYPTION_ENABLED=no
- SPARK_SSL_ENABLED=no
- SPARK_USER=spark # 运行用户
ports:
- '8080:8080'
spark-worker:
image: docker.io/bitnami/spark
environment:
- SPARK_MODE=worker
- SPARK_MASTER_URL=spark://spark:7077 # 通过 SPARK_MASTER_URL=spark://spark:7077 连接到主节点
- SPARK_WORKER_MEMORY=1G # 分配 1GB 内存
- SPARK_WORKER_CORES=1 # 分配 1 个核心。
- SPARK_RPC_AUTHENTICATION_ENABLED=no
- SPARK_RPC_ENCRYPTION_ENABLED=no
- SPARK_LOCAL_STORAGE_ENCRYPTION_ENABLED=no
- SPARK_SSL_ENABLED=no
- SPARK_USER=spark
运行集群
cd spark
docker-compose up --scale spark-worker=3 -d
docker-compose logs spark
docker-compose stop spark
提交测试程序
docker exec -it 06e7aa696ece /bin/bash
alias ls='ls --color'
spark-submit examples/src/main/python/pi.py
案例程序
from pyspark.sql import SparkSession
spark = SparkSession.builder.appName("SparkExample").getOrCreate()
data = [1, 2, 3, 4, 5]
rdd = spark.sparkContext.parallelize(data)
# 显示 RDD 中的数据
# print(rdd.collect())
data = [("Alice", 25), ("Bob", 30), ("Cathy", 28)]
columns = ["Name", "Age"]
df = spark.createDataFrame(data, columns)
df.createOrReplaceTempView("people")
# 执行 SQL 查询
result = spark.sql("SELECT * FROM people WHERE Age > 25")
# 显示查询结果
result.show()
一些随笔
人生为什么这么纠结
作为人,一种纯粹的精神存在,意义可以向着自我、内在无限延申,每个人的一生都是无限种可能,每个独立的人都可以握住评价自己的标尺,评价自己所做的一切,甚至可以没有评价的概念,无论什么行为,就是意义本身,就是价值本身,目的和手段统一,结果和过程统一,可以不再追问,可以潇洒人生。但是在面临无限的选择时,没有权威性的指引,需要主观创造意义,一个人如果在完全主观的系统中去追寻意义,会像在无边的虚空中航行,个体容易彷徨、迷失,人生变得索然无味。
作为动物,繁衍的本能和对安全感、确定性的追求,让我们每个人潜意识都认识到,个体有很大一部分的价值判断在自我的外围,渴望得到同性的认可,渴望得到异性的青睐。
外部价值评价,往往会在整个社区形成一种较为稳定的共识,比如金钱、外貌、学识等,每个人都有确定的、相似的目标。当我们追求动物性欲望时,我们的欲望往往指向的是有限的资源,群体就会竞争,内卷,会很累,我们主动把评价的权力交付出去,个体就会妥协,谄媚,我们的人生也会变得越来越雷同。
我们基本不能在不牺牲一个目标的情况下,提升另一个目标。人就活在这种张力中,既希望忠于自我,又希望被外界认可。