循环神经网络

对于传统的神经网络，在进行前向计算时，各次调用之间是相互独立的。例如，对两张图片进行分类时，第一次的分类结果不会影响第二次的识别过程，二者是完全分离的运算。因此，这类神经网络通常要求输入的维度保持完全一致。

然而，有些任务的输入维度并不固定。例如，提取一句话中与时间相关的描述时，不同句子所包含的词数往往不同，这就带来了输入长度不一致的问题。对此，常见的一种解决方法是“补齐”，即将所有句子强制调整为相同的长度：不足的部分用空白填充，超出的部分则予以截断。这种方法虽然简单直接，但显得不够优雅。

另一种思路是将任务切分为一致的最小输入单元，例如逐字处理。基于此，可以设计一种神经网络，使其每次仅处理一个字，同时通过某种机制将前一次处理得到的信息传递到当前步骤，从而在保持输入长度灵活性的同时，实现上下文之间的关联。

循环神经网络（Recurrent Neural Networks, RNN）很好地解决了输入维度不一致的问题。RNN 的结构中引入了循环机制，使得网络能够在时间维度上传递和保留信息（这里的时间维度，只是一种顺序而已）。

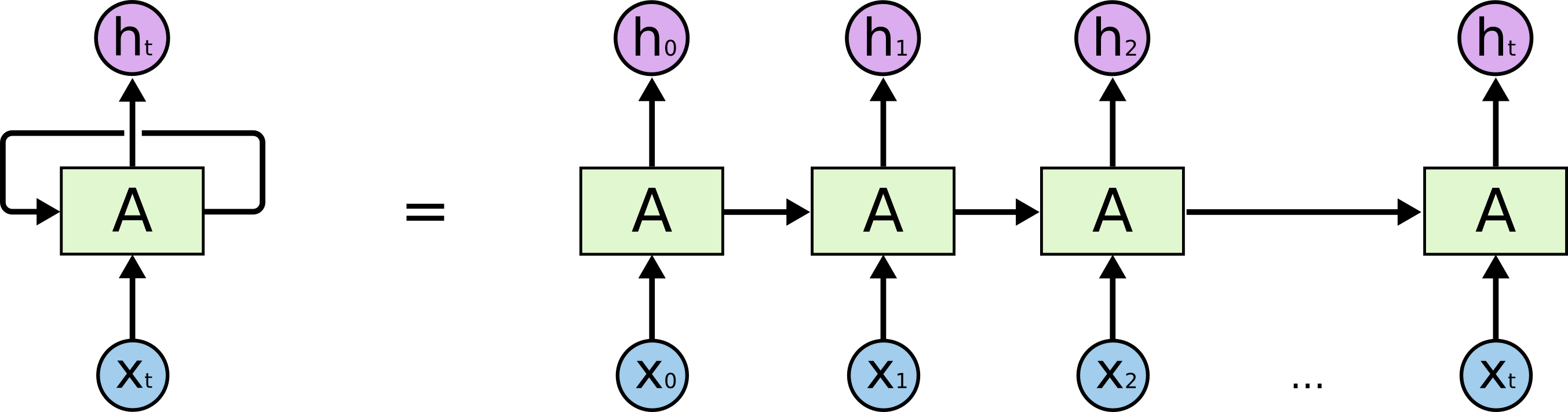
循环神经网络最核心的思想是延展输入向量（不仅仅看现在的词，还要看上文），同时输出一个前文压缩信息给后续的调用使用（上文哪里来？一种标准的网络结构在存储上文信息）。

循环神经网络应用很广法，这些成功的关键在于使用了“LSTM”，一种非常特殊的循环神经网络，它在许多任务中比标准版本表现得好得多。几乎所有基于循环神经网络的令人兴奋的结果都是通过它们实现的。正是这些 LSTM 将是本文探讨的内容。

LSTM 的数学表达式

一个 LSTM 神经元相当于四个普通神经元。

输出神经元（和普通的神经网络没区别，只是扩展了上下文） \[ o_t = \sigma(W_o x_t + U_o h_{t} + b_o) \]

输入神经元 \[ i_t = \sigma(W_i x_t + U_i h_{t} + b_i) \]

遗忘神经元 \[ f_t = \sigma(W_f x_t + U_f h_{t} + b_f) \]

记忆神经元 \[ c_t = f_t \otimes c_{t-1} + i_t \otimes \sigma(W_c x_t + U_c h_{t} + b_c) \]

隐藏状态 \[ h_{t+1} = o_t \otimes \sigma(c_t) \]

其中，\( h_0 = 0 \)

LSTM 神经元可以横向排列，组成 LSTM 层。不同的神经元可以从输入序列中提取上下文信息的不同方面，从而实现更丰富的特征表示。

训练用时间反向传播，还是利用链式求导法则进行推导，与一般的神经网络不同，其梯度来源不仅仅是某一个网络的调用，还来来至后一次某一个网络的调用传到的输入向量的梯度（\( h_t \)）。

循环神经网络的训练数据是 \( k\) 个输入输出对的有序序列。

\[ <x_0, y_0>, <x_0, y_0> ... \]

首先按顺序前向运行一个循环神经网络，运行后的神经网络包含 \( k\) 个输入和输出。

\[ <x_0, h_0 , \hat{y}_0, h_1>, <x_1, h_1, \hat{y}_1, h_2> ... \]

但每个网络副本都共享相同的参数。然后，使用反向传播算法求出损失函数相对于所有网络参数的梯度。