物质导数
在流体力学研究中,我们通常关心流体中的物理量(如密度 ( \rho )、速度 (\mathbf{v})、温度 (T) 等) 如何随时间和空间变化。为了描述随流体运动的某一点的性质变化, 我们引入物质导数(Material Derivative)。
物质导数是沟通拉格朗日法和欧拉法的核心公式。 拉格朗日法关注的是随流线移动的流体微元内部的属性。 欧拉法关注的是三维空间中固定位置的微元内部的属性。
物质导数是沿着流线的变化率(全导数)。
流线是关于时间的函数(关于时间的参数方程)。 [\mathbf{x} = \mathbf{x}(t)]
随着流线移动的微元的属性可以表示为 [\rho = \rho(\mathbf{x}(t), t) ]
物质导数就是对随流线移动的流体微元的属性求时间的导数, 根据多元函数的微分法则可知。
[ \frac{D \rho}{ D t} = \frac{\partial \rho}{\partial t} + \frac{\partial \rho}{\partial \mathbf{x}} \frac{\partial \mathbf{x}}{\partial t} = \frac{\partial \rho}{\partial t} + \mathbf{v} \cdot \frac{\partial \rho}{\partial \mathbf{x}} ]
要理解该公式,首先要注意, 随流线移动的流体微元 是一个随时间移动的立方体 (一个纯粹的几何体,可以是其他形状的微元,但是必须是微分体积), 当时间固定时,随流线移动的流体微元 会与 一个 三维空间中固定位置的微元 重合。

微元并不是包含流体的一个流体团(只是一个形状不变的几何体),因此,其体积内部并不是质量守恒的。 随流线移动的流体微元 内部的属性随时间的变化(比如密度) 包含两个部分,一部分是与当前随流线移动的流体微元重合的 三维空间中固定位置的微元的属性变化 (没有源汇的情况,微元表面的通量导致局部变化)。 另一部分是微元随着流线移动一小步(微元的位置会随时间变化)导致的变化。
[ \frac{D \rho}{ D t} = \frac{\rho_{t+\Delta t}^{trace} - \rho_{t}^{trace}}{\Delta t} ] 其中,$\rho^{trace}$ 是指随流线移动的流体微元的密度 [ \frac{\partial \rho}{\partial t} = \frac{\rho_{t+\Delta t}^{local} - \rho_{t}^{local}}{\Delta t} ] 其中,(\rho^{local}) 是三维空间中固定位置的微元的密度
注意,在 (t) 时刻,随流线移动的流体微元与三维空间中固定位置的微元 重合。 因此 (\rho_{t}^{trace} = \rho_{t}^{local}) [ \frac{D \rho}{ D t} - \frac{\partial \rho}{\partial t} = \frac{\rho_{t+\Delta t}^{trace} - \rho_{t+\Delta t}^{local}}{\Delta t} ]
在 (t+\Delta t) 时刻,随流线移动的流体微元与三维空间中固定位置的微元 不重合。 存在偏移, 偏移量与流体微元在 (t) 到 (t + \Delta t) 时刻的速度相关
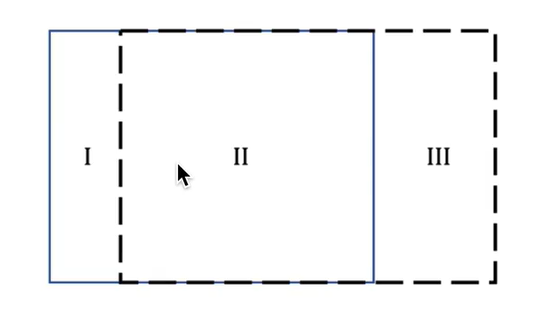
[ \rho_{t+\Delta t}^{trace} - \rho_{t+\Delta t}^{local} = \frac{\int\limits_{t}^{t+\Delta t} v(t), dt}{\Delta x} (\rho_{t+\Delta t}^{local+\Delta x} - \rho_{t+\Delta t}^{local}) ]
根据积分中值定理, 由于 (\Delta t \to 0) [ \int\limits_{t}^{t+\Delta t} v(t), dt \approx v_t \Delta t ]
因此 [ \frac{\rho_{t+\Delta t}^{trace} - \rho_{t+\Delta t}^{local}}{\Delta t} = v_t \frac{\rho_{t+\Delta t}^{local+\Delta x} - \rho_{t+\Delta t}^{local}}{\Delta x} = v_t \frac{\partial \rho}{\partial x}|_{t=t+\Delta t} ]
可得 [ \frac{D \rho}{ D t} = \frac{\partial \rho}{\partial t} + v_t \frac{\partial \rho}{\partial x}|_{t=t+\Delta t} ]
根据泰勒展开,且 (\Delta t \to 0),最后可得一维的情况 [ \frac{D \rho}{ D t} = \frac{\partial \rho}{\partial t} + v \frac{\partial \rho}{\partial x} ]
物质导数的意义
可以根据物质导数定义一些特殊的流体,比如可以给出不可压缩流体的定义为 [ \frac{D \rho}{ D t} = 0 ] 如果是一维情况,不可压缩流体意味着流体本身运动与微元的运动是一致的。
根据连续性方程, [ \frac{D \rho}{ D t} = - \rho \nabla \cdot \mathbf{v} = 0 ]
不可压缩流体并不意味着流体性质均一,因此 (\rho \neq 0), 所以可得 [ \nabla \cdot \mathbf{v} = 0 ]
如果只看二维的情况 [ \nabla \cdot \mathbf{v} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 ] 也就意味着在 $x$ 方向的压缩,会导致在 $y$ 方向膨胀。
同时物质导数直观的反映了沿着流线的属性变化, 比如一根流线分别在三点和四点经过的苏州上海。 苏州三点温度为 20 度,上海四点维度为 21 度。 可以认为 20 度是温度平流, 而多出来的 1 度是气团在流动过程中被加热了(热传导、做工、热辐射等)